

Introduction
Cryptographic attacks, even more advanced ones, are often made more difficult to understand than they need to be. Sometimes it’s because the explanation is “too much too soon” — it skips the simple general idea and goes straight to real world attacks with all their messy details. Other times it’s because of too much formalism: it’s \(m^e\) this and \(m^{ed}\) that, without any regard for where these came from or what they signify.
The line between a “classic” and a “modern” cryptographic attack can be blurred. However, most people would agree that (for example) differential cryptanalysis is not like a basic frequency analysis. The mathematics involved is more complicated, the era of cryptography that gave rise to the attack is more rugged and mature, and it’s much harder to explain the attack to a seventh-grader and have them exclaim “I could have thought of that”. Regardless, even these attacks can be perfectly easy to understand, once they are explained plainly.
In this write-up, we lay out in simple terms:
- “Classic Flavor” modern cryptanalysis (e.g. meet-in-the-middle attacks, Birthday Attack on CBC)
- Statistical Bias Attacks (e.g. differential cryptanalysis, FMS attack on RC4)
- Side Channel Attacks (e.g. Timing Attacks, an honorable mention for SPECTRE)
- Attacks on RSA (e.g. Bleichenbacher’s attack, related message attacks, Coppersmith’s method)
For more attacks and more explanations see our earlier report Cryptographic Attacks: A Guide for the Perplexed.
Classic-Flavor Cryptanalysis
Meet-in-the-Middle Attack
DES, designed by IBM, can be considered to be the cipher that kicked off the modern era of cryptography. We’ll mention DES a few more times below (and if you are really curious, this write-up is an excellent read), but one of its properties was that its key-length was nerfed post-design to a mere 56 bits, due to — as Schneier puts it in the above link — the “invisible hand of the NSA”. Not long after the DES spec was published, the same team lead at IBM who oversaw the original design offered an improved design for people who were understandably troubled by the reduced key length: Triple-DES (3DES). Choose 3 different 56-bit keys and transform the plaintext with all three, one after the other (we’d say “encrypt three times” but actually it’s encrypt-decrypt-encrypt; see here). Effectively, this transforms DES into a cipher with a \(56 \times 3 = 168\) bit key, at the cost of tripled computation time.
You may naturally ask, what about 2DES? Where did 2DES go? The answer has to do with something called a “meet-in-the-middle attack”. This attack isn’t concerned with the exact cipher being used (for our purposes, the cipher used (e.g. DES) is a magic black box that performs encryption). It makes use of what’s called a “space-time trade-off”. What this means is that with access to a great amount of storage space, an attack can do more with less time.

The extreme form of this principle is that you could theoretically break a modern cipher, for example AES, by encrypting every single possible plaintext using every single possible key, and then creating a gigantic precomputed table that records the correct encryption key for each possible pair of plaintext and ciphertext blocks (for a modern cipher, this level of break is considered Very Bad). However, there are several technical snags in this plan, one of them being that to store the resulting table for AES, you would need ten million SSD drives each having the mass of the universe. So, the trick isn’t so much to find any space-time trade-off as it is to find one that gives a usable time improvement while keeping the ‘space’ part feasible. (As an aside: due to the smaller key size of DES, building a table like this for it is practical, and has actually been done. You encrypt the specific plaintext 1122334455667788, hand the resulting ciphertext to the table, and get the key back in less than a minute. As mentioned above: Very Bad!)
Eve can use this “space-time trade-off” idea to attack 2DES. That is, if there are two keys \(k_1\) and \(k_2\) with a total key length of \(56 \times 2 = 112\) bit, and encryption proceeds by DES encryption with \(k_1\), then again with \(k_2\), then Eve has an attack strategy better than just blindly trying every possible combination of \(k_1\) and \(k_2\) (a “brute force attack”). The strategy works by abusing a certain property of the structure of 2DES — the fact that encrypting the plaintext with \(k_1\) will result in the same value as decrypting the ciphertext with \(k_2\) (you might want to stop for a minute and think about this; see the figure below).
Eve begins by obtaining some plaintext and its corresponding ciphertext. This is called a “known-plaintext” attack, and is generally considered feasible. She then encrypts the plaintext with every possible \(k_1\) and records every result in a database. This requires \(2^{56}\) operations, and about the same amount of memory. She then proceeds to decrypt the ciphertext with every possible \(k_2\) and checks every result to see if it’s in the database she created. Eventually, she will stumble on the correct \(k_2\); the decryption result will be in the database, left there from when Eve encrypted the plaintext with the correct \(k_1\) earlier. This search for \(k_2\) also requires \(2^{56}\) operations in the worst case. Therefore, Eve needed \(2^{56}+2^{56}=2^{57}\) operations in total, which is much fewer than the full \(2^{112}\) required for a brute-force attack. The attack effectively reduces 2DES security-wise to the same realm as regular DES. The cost was using an additional \(2^{56}\) bit of memory; the phrase “space-time trade-off” might feel more understandable now.
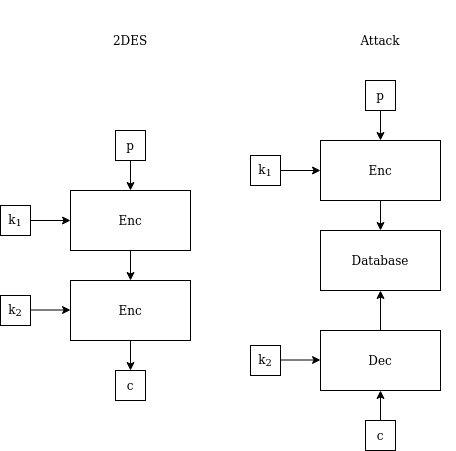
In a hypothetical world that adopted 2DES and made it an encryption standard, this “merely technical, hypothetical attack” would very quickly have become a reality. \(2^{56}\) bits of storage space may sound like a lot, but currently Google’s total storage is estimated to be several dozens times that.
Hence, the world went straight to 3DES, which itself reached its official end-of-life on December 31, 2023. Though DES will doubtless remain alive for some time to come — in our hearts, in legacy machines, and in the minds of exasperated students who fifty years from now will still be quizzed on this attack and how it cancelled 2DES a century before.
Birthday Attack
Maybe you’ve heard this one. Twenty-three random people walk into a room — what is the probability that at least two of them share a birthday? Most people answer somewhere between 1% and 10%, but that’s wrong. The answer is about 50%. (Forget for a moment about uneven birthday distributions, leap years, and so on.)
One way to see it is to imagine that we send these 23 people into the room one after another. The second person to walk in will match a birthday already in the room with probability \(\frac{1}{365}\), the third person with probability \(\frac{2}{365}\), and so on 23 times. For the several final people, the chance of collision is as high as 6% per person.

Another way to think of it: suppose we’d asked instead, “250 random pairs of people walk into a room — what is the probability that at least one of the pairs shares a birthday?” The answer “about even” sounds much less like it comes out of nowhere now. But consider that there are that many different pairs of people in the room! Alice and Bob are a pair, Alice and Charlie are a pair, and Bob and Charlie are a pair too, and so on. Even though there are only 23 people in the room, there are… How many possible pairs again? Let’s do the math: there are 23 options to pick the first person, multiplied by 22 options left to pick the second person, divided by 2 because this way we’ve counted every pair twice (once with Alice first and Bob second, and once the other way around). With 23 people in the room, that comes out to a full \(\frac{23 \times 22}{2} = 253\) pairs.
This calculation works just as well if we change the number of people in the room to whatever \(n\) we like: the possible number of pairs is going to be \(\frac{n \times (n – 1)}{2}\). If you expand that, that’s in the ballpark of \(n^2\) or so, and it gets out of hand pretty quickly. Forty-six people make over a 1,000 pairs. 142 people make over 10,000 pairs. 1,415 people make over a million pairs.
At this point you’re probably asking where the cryptographic attack is. To satiate your curiosity, we will show two.
Birthday Attacks on Digital Signatures
This is the most immediate — one might say “textbook” — application of birthday attacks.
Digital signatures are a handy way to verify the authenticity of messages and documents. To implement digital signatures, you typically need public-key cryptography. This kind of cryptography is costly to compute and has all kinds of mathematical properties that allow interesting attacks (as you will see later, when we discuss attacks on RSA). Therefore, instead of applying digital signatures to a whole object (like a document, or an executable file), it is customary to first pass the object through something called a hash function. This function takes the object and spits out a short “digest” that has a known, fixed length. For the example below, the output hash length is 60 bits.
Suppose that Alice has signed a document. To understand what’s going to happen next, you don’t need to know how this works exactly, just that Alice has a key that makes it easy for her alone to compute this signature. To be more precise, as we mentioned above, Alice computes the digest of the document, which she signs, and publishes the document and the signature.
Eve naturally gets a hold of the document and signature, and she hatches a scheme. She will create some nefarious document that Alice would definitely never sign, but has the same hash digest as Alice’s original document. As Alice signed the digest, not her original document, Alice’s signature is valid for both the “nice” document and the “naughty” one, and Eve can attach Alice’s signature to her own “naughty” document and pass it off as signed by Alice.
Of course, it’s not that easy. The thing with these hash functions is that they are specifically designed so that it is difficult to find a different document with a given hash. In fact, let us assume that in this case the hash function is built well enough to make this feat impossible. Still, Eve does not despair, and soon she has an idea.
This is where the “Birthday Attack” per se begins. Eve generates \(2^{30}\) messages that are all variations of her “naughty” document. This isn’t difficult to do: a phrasing can be changed here, some spacing can be changed there, and soon there’s an explosion of possibilities. More importantly, \(2^{30}\) is a much, much smaller number than \(2^{60}\) — a number Eve’s laptop (and yours) can deal with. With that done and the “naughty” set of messages produced, Eve now turns around and does the same thing again, this time generating a “nice” set: \(2^{30}\) variations on some completely innocuous document that Alice would be happy to sign, suspecting nothing.
What is the chance that at least one pair of messages, with one message from the “nice” set of \(2^{30}\) and the other from the “naughty” set of \(2^{30}\), share their hash function digest, which is taken randomly from a pool of \(2^{60}\) values? Just like in the “birthday” example, it’s about a 50% shot. And if it fails, Eve can just try again.
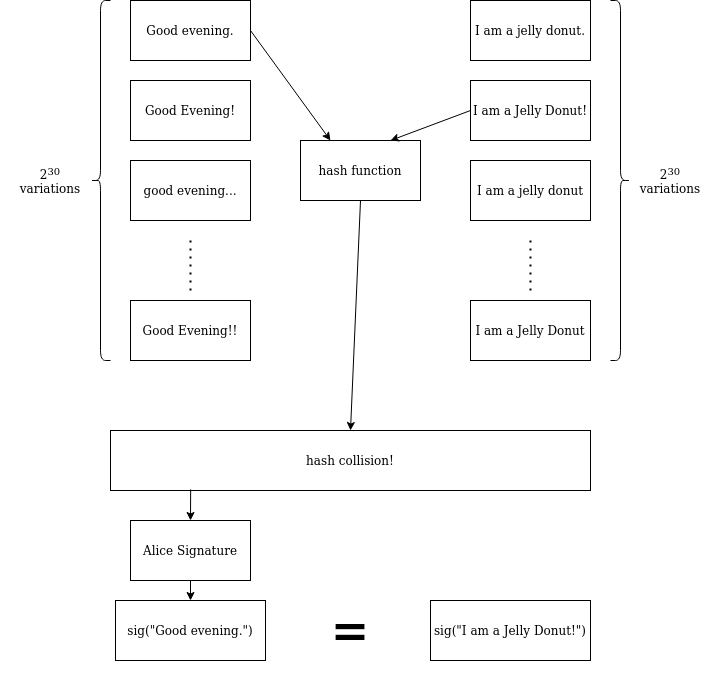
Using this procedure, Eve obtains a “nice” message and a “naughty” message that share the same digest. She gets Alice to sign the “nice” message and Alice agrees, suspecting nothing. A day later, the “naughty” document surfaces, containing something embarrassing in proud bold font. To Alice’s great alarm, it carries her valid signature. The person she is currently dating begins ghosting her, and she spends the rest of her life wondering what malicious prankster has done this to her, and how.
This is why we have SHA-256, with its 256-bit output length, and not SHA-60.
Birthday Attack on the CBC Mode of Operation
What is CBC?
A “block cipher” is a cipher which takes a key and input of a certain fixed length (the “block length”) and outputs an encrypted block of the same length. Block ciphers are widely used, and are considered relatively secure, all other things being equal. The now-retired DES, widely considered the first modern cipher, was a block cipher, as is AES which is used extensively today.
Unfortunately, block ciphers have one glaring weakness. The typical block size is 128 bits, or 16 characters. Obviously, in the information age, you want to work with longer inputs, and this is where modes of operation come in. A mode of operation is basically a hack — an algorithm that takes a block cipher, which can only handle a fixed amount of input, and somehow makes it work with inputs of arbitrary lengths.
These modes of operation seem to be the weak link in the application of block ciphers. Successful, practical attacks on modes of operation are much more common than attacks on the underlying ciphers. For example, the straightforward mode of operation ECB (Electronic Code Book — just encrypt normally block-wise) is known as a bad choice because it transforms equal plaintext blocks into equal ciphertext blocks, and this allows attackers to see the penguin.

The issues with ECB are well-known enough that the go-to alternative for many simple use cases is another mode of operation, CBC (Cipher Block Chaining). This diagram illustrates how CBC mode operates:
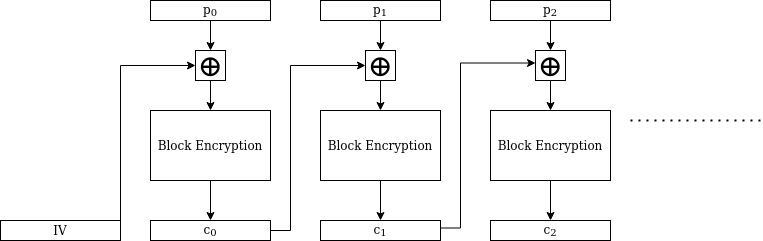
The circled plus sign \(\oplus\) stands for the XOR operation. So, for example, the second ciphertext block is obtained by:
- XORing the second plaintext block with the first ciphertext block.
- Encrypting the resulting block with the block cipher, using the key.
Unfortunately, CBC mode itself is also subject to some attacks. One well-known example is the “padding oracle” attack (an in-depth explanation for it is available here).
As CBC makes such heavy use of the XOR operation, let us take a moment to recall the following useful properties of XOR.
- Identity: \(A \oplus 0 = A\)
- Commutativity: \(A \oplus B = B \oplus A\)
- Associativity: \( (A \oplus B) \oplus C = A \oplus (B \oplus C) \)
- Involution: \( A \oplus A = 0 \)
- Bytewise: \( \text{byte n of }(A \oplus B) = (\text{byte n of }A) \oplus (\text{byte n of }B) \)
These properties imply that if we have an equation involving XORs and some unknowns, it’s usually possible to solve for the XOR of the unknowns. The simplest example is with one unknown: if we know that \( A \oplus X = B \) with \(X\) the unknown and \(A\), \(B\) known, we can rely on the properties above to solve for \(X\): XOR both sides of the equation with \(A\) and obtain \(X=A \oplus B\). Using a similar technique, if we have the equation \( A \oplus X = B \oplus Y \) and we know \(A\), \(B\) , then we can rearrange the equation to read \(X \oplus Y = A \oplus B\). This will become relevant in a short moment.
The Attack
We’ll emphasize here again that this is not an attack against a particular cipher like DES or AES — it applies to any block cipher when used in CBC mode.
Suppose that a block cipher has a length of n bit. Alice keeps encrypting all sorts of plaintexts using that cipher in CBC mode, and Eve wants to mount an attack and reveal the original plaintext.
From Eve’s point of view as an attacker, the ciphertext blocks appear effectively random. But she can turn this to her advantage, and apply the birthday paradox. She knows she can eventually expect two random ciphertext blocks to “collide” and have the same value. She even knows how many blocks Alice needs to encrypt before the chance of a collision becomes reasonable — about \(\sqrt{2^{n}} = 2^{\frac{n}{2}}\) blocks or so. For example if \(n= 64\), Alice would need to encrypt several GB of data (not common but still possible).
Let’s say Alice encrypts many plaintext blocks, starting with with \(p_0, p_1, p_2, \ldots\) and resulting in the ciphertext blocks \(c_0, c_1, c_2, \ldots\) respectively. Eventually after doing this for several GB of data, a collision occurs and we have, say \(c_{908} = c_{1404}\) . Now perform a block decryption on both sides of this equation, and obtain \(c_{907} \oplus p_{908} = c_{1403} \oplus p_{1404} \) (if this seems complicated, the below diagram should help greatly). In that equation, Eve knows two values (the c values) and doesn’t know two other values (the p values). We just stated what this allows her to do — solve for the XOR of the unknowns, that is, for \(p_{908} \oplus p_{1404}\). Obtaining the XOR of two plaintext blocks easily allows for teasing out the original blocks themselves (this involves a technique called frequency analysis which we will not dive into here. It’s sufficient to say that the technique has been known since early in the 20th century, and has been used to break ciphertexts of an improper repeat use of a one-time pad).
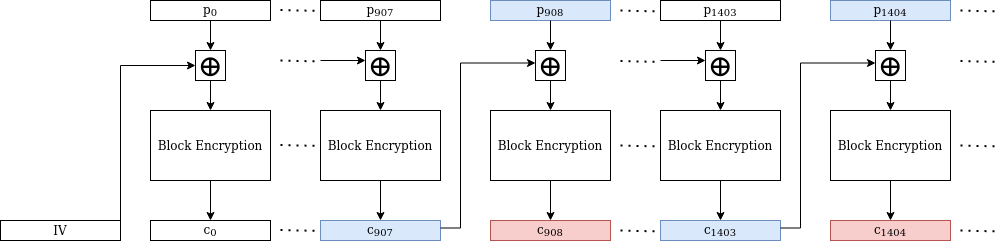
This attack might seem purely theoretical, but it did see an application with very real consequences. Recall the story of 3-DES: it was created to mitigate the small key size of DES, but the block size remained the same, 64 bit, in contrast with the 128 bit typical of more modern ciphers (like AES). In 2016, Bhargavan and Leurent introduced Sweet32, a birthday attack targeting a wide array of protocols (including HTTPS and OpenVPN) that made use of ciphers that had a block length of 64 bit. In their own words:
We show that a network attacker who can monitor a long-lived Triple-DES HTTPS connection between a web browser and a website can recover secure HTTP cookies by capturing around 785 GB of traffic. In our proof-of-concept demo, this attack currently takes less than two days, using malicious Javascript to generate traffic.
The National Institute of Standards and Technology specifically cited the Sweet32 attack in its decision to deprecate 3DES and disallow its use in modern internet protocols. In other words, this specific birthday attack was a big factor in the death of the first modern cipher.
Statistical Bias Attacks
Shannon Deprogram
When doing cryptanalysis, in a narrow certain sense, “information” is cheap — you already have all the “information” you need, and it is all useless.

This must sound strange — after all, when doing cryptanalysis, it’s common to talk about how the ciphertext “leaks information” on this, or the server behavior “leaks information” on that. But, remember that earlier we discussed how you can theoretically break AES with a precomputed table that maps (plaintext, ciphertext) pairs to keys. Now note that while this table is too large to actually compute and store, it is not a secret. You have all the information you need to compute it. So, you see, the moment you are handed the plaintext and the ciphertext, you already know the key — from a certain point of view.
This is the well-known framework of Information Theory, as formalized by Shannon. In this framework “information” means lack of uncertainty, and uncertainty means not only you don’t know, but you can’t know, even if you looked at the information available to you with infinite all-knowing wisdom. For example if someone flipped a coin and didn’t tell you the result, then you would have actual uncertainty. On the other hand if you had information that determined the coin toss result, you’d “know” that result — even if “following the logic” would require a computation lasting \(2^{2048}\) years (or is in some sense impossible — the contents of a program determine whether it terminates or not, but good luck writing an algorithm to compute that!)
When doing cryptanalysis, to “have information” it is not enough to have it in the Shannon sense. You must have a feasible algorithm capable of expressing this information; a giant, universe-sized precomputed table doesn’t cut it. In the context of cryptanalysis, when we say “\(X\) leaks information in \(Y\)” what we really mean is: “if Alice knows \(X\) and Bob doesn’t, Alice’s best feasible algorithm to guess the value of \(Y\) is going to perform better”. Without access to a plaintext or ciphertext, Bob’s best feasible algorithm is to pick a key at random and hope for the best. Therefore, if Alice’s best feasible algorithm can do any better, that is considered a cryptanalytic information leak.
More often than not, we know some feasible algorithm for Alice to do at least a little better than a completely blind guess. To prevent this from having bad consequences, we rig the encryption scheme parameters (key length, number of rounds…) so that even with this advantage, the attack can only get so far as a cryptographic achievement, without any further real world implications. For example, suppose that tomorrow a grad student finds an attack that uses information leaks in the AES-256 cipher design to reduce its effective key size from 256 to 200 bit. Explaining the value of this to a journal review panel is going to be fairly easy; explaining the immediate value of it to a military SIGINT unit, maybe not quite so easy.
In conclusion, plaintexts and ciphertexts leak plenty of information on the key in the Shannon sense, but usually we can only express a small fraction of this leak in terms of a feasible algorithm. Being able to express the whole information leak this way will typically mean that the cipher in question is broken. From now on, when we say “information leak”, we mean it in the cryptanalytic sense.
Basic Statistical Bias Attacks

The principle of exploiting statistical biases in ciphers is universal and has many varied applications. We’re going to see two flavors here: “visible bias event” attacks that look for evidence of some event that cuts down the space of possible keys, and “direct” attacks that allow direct recovery of key bytes.
To demonstrate the attacks in this section we’re going to use a hypothetical toy block cipher, which we’ll call TBC for short. This cipher has both a block length and key length of 256 bit (the specific number doesn’t matter so much for the purposes of the attack). We will see three attacks, in increasing order of complexity.
Let’s start with something straightforward. Assume for a moment that TBC has an “even XOR property”: the XOR of the plaintext, ciphertext, and key is always even. This implies the plaintext and ciphertext leak information on the key. Specifically, if Eve is trying to attack TBC encryption, she can make her mission easier if she gets her hands on just one pair of plaintext and ciphertext. If their XOR is even, then so is the key. If their XOR is odd, then (again) so is the key. Instead of blind brute force search, Eve can accordingly try just the even keys or just the odd keys, cutting the required time of the attack by half.
Let’s try a slightly more complicated scenario. Suppose that for every TBC key, only 1 in 10,000 plaintexts will have this vulnerable “even XOR property”. Further suppose that when the even XOR property emerges, it is instantly recognizable from looking at the plaintext and ciphertext. Eve can easily still mount an attack: she starts generating and encrypting plaintexts until one of the encryptions visibly triggers the even XOR property. From there, she proceeds exactly as before, deducing whether the key is even or odd, and using that information to discard half of all keys as irrelevant. Eve had to perform an extra 10,000 encryptions or so, but this shaved off a full \(2^{255}\) keys from a full brute force attack — a very worthwhile trade-off.
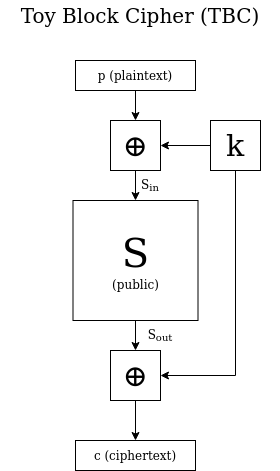
The interesting thing is that this kind of attack can still work with an information leak on some encryption internal state, without even placing an explicit constraint on the key. To explain what we mean by this, let’s give a more detailed construction of TBC — one that proceeds in three stages, as seen in the accompanying figure:
- A XOR with the secret key K
- Some publicly known function S that transforms 256-bit blocks to other 256-bit blocks
- a XOR with K again
Now let’s suppose that the function \(S\) has an inherent statistical bias: for a random input block \(S_{\text{in}}\), the probability that \( S_{\text{in}} \oplus S_{\text{out}} = \text{0x800} \) is \(\frac{1}{2^{120}}\), instead of \(\frac{1}{2^{256}}\) as you would expect if \(S\) behaved in an ideally random fashion. In other words, instead of exactly 1 value of \( S_{\text{in}} \) that has \( S_{\text{in}} \oplus S_{\text{out}} = \text{0x800} \), there are \(\frac{2^{256}}{2^{120}} = 2^{136}\) such values.
Before we proceed to show what Eve can do with this information, we need to point out 2 important details:
- Directly due to the way TBC is built, we have \( S_{\text{in}} \oplus S_{\text{out}} = p \oplus c \). Therefore, when Eve encrypts a plaintext and obtains the resulting ciphertext, she can also compute \( S_{\text{in}} \oplus S_{\text{out}} \), a piece of information about the internal encryption state.
- For a given plaintext and ciphertext, if Eve can guess \(S_{\text{in}}\), she can then deduce the encryption key \(k\). She can do this by applying \(S\) to \(S_{\text{in}}\) and thus obtaining \(S_{\text{out}}\); then XORing that value with the ciphertext \(c\). The result is \(k\), the key (we recommend you stop for a moment and think about this — probably the easiest way to see it is to carefully follow the diagram). Let’s call this the \(S \rightarrow k\) process.
Can Eve leverage these two points to mount an attack and recover the key \(k\) itself? Yes, and we will now explain in detail how. Just like she did before, Eve starts randomly generating and encrypting plaintexts, until finally she finds an “interesting” plaintext and ciphertext pair where \(p \oplus c = \text{0x800}\). This should take \(2^{210}\) encryptions or so (because it happens with probability \(\frac{1}{2^{210}}\)). Now, Eve narrows her focus to the “interesting” pair she just found and its specific encryption process. She makes use of the fact that there are only \(2^{136}\) possible values of \(S_{\text{in}}\) (the ones that result in the 0x800 phenomenon). So, Eve can perform a brute force search on these \(2^{136}\) possible values of \(S_{\text{in}}\), performing the \(S \rightarrow k\) process on each one, and eventually find the correct key.
Eve performed a total of \(2^{136} + 2^{120}\) encryptions, which is drastically less than the \(2^{256}\) required for a brute force search. That’s a cryptographic break! If you doubted the power of an information leak on the encryption internal state before, you should be able to properly appreciate it now. Many other attacks operate on the same principle — for example, Davies’ Attack on DES.
Again, we emphasize that unlike with the “even XOR” scenario, Eve was able to mount her attack without an explicit constraint on the key. Indeed, the data leak that Eve used, \( S_{\text{in}} \oplus S_{\text{out}} = p \oplus c \), bypasses the key and factors it out of the equation. It was enough that \( S_{\text{in}} \oplus S_{\text{out}} = \text{0x800} \) functioned as a “visible bias event”, meaning it was:
- On the one hand uncommon enough that triggering it disclosed a lot of information on encryption internal state.
- But on the other hand, common enough that it could be reliably triggered with fewer encryptions than a full brute force.
- Visible to an attacker with access to only the plaintext and the ciphertext.
Any event with these three characteristics is enough for Eve to mount an attack using the same attack plan.
Modern ciphers are not “toy” ciphers. Their design makes it typically difficult to find visible bias events as straightforward as the one we found for TBC. TBC was simple enough that Eve got lucky and was able to “cancel out” the masking effect of the two XOR operations, but in more complex cipher design, these XORs will typically hide most statistical cues coming out of the publicly known “S” transforms. Surprisingly, even in these more difficult cases, sometimes the attack can still be rescued, using a technique that we will describe below.
Differential Cryptanalysis
We now find ourselves in a strange land, one where we figuratively encrypt things that aren’t really there, and get a different result from what we’d get if they really were there and we’d actually encrypted them. The key insight here is this: instead of looking at one plaintext, Eve looks at two plaintexts, and observes what happens to their difference (XOR) during the encryption process.
An important aside is that a proper cryptosystem will usually have some kind of key scheduling in place so that each XOR is not with the key \(k\), but instead with the next value in some list of values derived from \(k\) using a key scheduling algorithm, with each value used once. So for example the cipher runs this key scheduler on \(k\) and obtains a list of subkeys \(k_0, k_1, k_2, \ldots\) and then instead of XORing each time with \(k\) (as seen in TBC), when a XORing operation is first required, the algorithm will XOR with \(k_0\), then the next time with \(k_1\), and so on.
This is important to understand because in difference-land, even these clever “scheduled” XOR operations have absolutely no effect. The initial plaintext difference is some \( p_1 \oplus p_2 = \Delta_0 \). After that first XOR operation is applied to each plaintext, the difference now equals \( (p_1 \oplus k_0) \oplus (p_2 \oplus k_0) \), which is again \( p_1 \oplus p_2 = \Delta_0 \), the exact same as before. Similarly, every XORing that happens afterwards doesn’t change the incoming \(\Delta\) value. (Obviously, this also applies to TBC and its simpler mechanism of just XORing with \(k\) every time.)
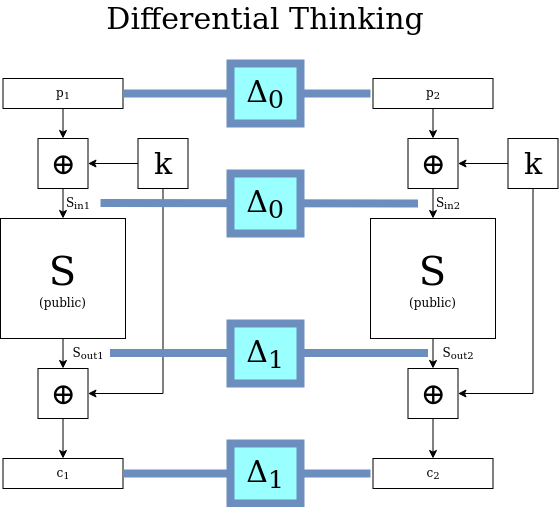
It’s the second TBC stage — applying the publicly-known transform \(S\) — that gets more complicated when we’re talking about differences. If we are looking at a given \(p_1\) and \(p_2\) then it’s straightforward: their difference \(\Delta_0\) comes in, and some other difference \(\Delta_1\) comes out, as depicted in the figure above. But generally, outside the context of a given \(p_1\) and \(p_2\), what does it mean for \(S\) to act on a difference such as \(\Delta_0\)?
It’s tempting to get caught up in this thinking of \(\Delta_0\) coming in and a singular value \(S(\Delta_0)\) coming out, but we need to stay acutely aware of the fact that \(S\) does not literally operate on differences, only on concrete blocks, which are sequences of bits. There are many possible pairs \(x,y\) that have \( x \oplus y = \Delta_0 \). Maybe for instance \(x \oplus y = z \oplus w = \Delta_0 \), so the “input difference” to \(S\) is the same for both these pairs, but there is no guarantee at all that \(S(x) \oplus S(y) = S(z) \oplus S(w) \). This implies that the same “input difference” can map to many possible “output differences”. To visualize \(S\) acting on a difference, we need to simultaneously visualize all possible pairs that have that difference, and then for each pair, imagine \(S\) acting on the two members and creating two new values that have their own, new difference. This results in a sea of possible output differences in various proportions (maybe it helps to say “probability distribution” here, but if hearing that confuses you further, forget we said that). With that in mind, maybe the figure above is good when we’re thinking about specific values of \(p_1\) and \(p_2\) — but if we want to think about differences and how the cryptosystem acts on them in their own terms, maybe the figure below is better.
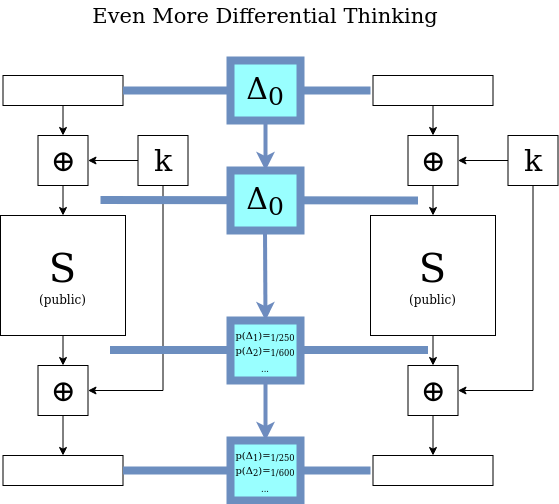
Now, how does all of this allow us to mount an attack?
Suppose there is a powerful bias in how \(S\) acts on (let’s say) \( \Delta = 17 \). There are \(2^{256}\) \( s_{\text{in1}}, s_{\text{in2}}\) pairs that have that difference. If \(S\) were truly random, we’d expect about 1 of these pairs to result in (let’s say) \( S(s_{\text{in1}}) \oplus S(s_{\text{in2}}) = 80 \). Instead, due to the bias, a full \(2^{100}\) of \(s_{\text{in1}}, s_{\text{in2}}\) pairs satisfy this property, which we will call the \(17 \rightarrow 80\) “differential”. Now, here are two interesting facts we already know about the \(17 \rightarrow 80\) differential:
- When picking two pairs \(p_1, p_2\) that have a difference of 17, the chances for the \(17 \rightarrow 80\) differential to occur are \(\frac{2^{100}}{2^{256}} = \frac{1}{2^{156}}\) .
- When a \(17 \rightarrow 80\) differential occurs, it is immediately visible to anyone with access to the plaintext pair and ciphertext pair, because the two XOR operations don’t affect the difference. The plaintext difference will be 17 and the ciphertext difference will be 80.
Do you see? We’ve magically conjured a “visible bias event”, and we’ve already seen that this allows an attack.
When DES was first published, many people suspected that its S-boxes were doctored somehow to contain a backdoor. Later it turned out that at the time when DES was designed, IBM already knew about differential cryptanalysis (which was not public knowledge) so the S-boxes were designed to be resistant to that specific attack. In other words, they were doctored exactly as everyone suspected, but with the goal of making the cipher stronger, not weaker. Differential Cryptanalysis was discovered independently by Biham and Shamir in the late 1980s, and finally made public knowledge.
FMS Attack on RC4
This is a very elegant attack, but the many involved details can make it easy to get lost and miss the forest for the trees.
To understand the attack, you must first understand how RC4 works in general. A “Key Scheduling Algorithm” (KSA) takes your key and generates a 256-byte array, and then a “Pseudo-Random Generation Algorithm” (PRGA) uses that byte array to output an endless stream of bytes (the “key stream”), which looks like random noise unless you know what the original byte array was. To encrypt a text, this key stream is XORed with a plaintext, and decryption is done by XORing the ciphertext with the key stream again.
Remember when we talked about how block ciphers in themselves are relatively secure, but the mode of operation employed for encryption of large amounts of data is the weak link? Multiply that sentiment by a million, and you get the situation with RC4. Technically it is difficult to mount an attack on RC4 if a large key is used exactly once, with attacker access to the ciphertext alone (and we even had our very own moment of temporary insanity dedicated to this matter in 2022). But you naturally want to use your key \(k\) more than once. This is a mistake.
Maybe you try a “simple mode of operation” just reusing \(k\) as-is for two plaintexts \(p_1\) and \(p_2\). This results in two ciphertexts \(c_1 = p_1 \oplus k\) and \(c_2 = p_2 \oplus k\). No luck: an attacker computes \(c_1 \oplus c_2 = p_1 \oplus p_2\), then uses that to recover \(p_1\) and \(p_2\) (again – recovering two plaintexts from their XOR is very possible). So you say, “I will salt \(k\) every time: choose some byte string which I’ll call the “IV”, prepend it to \(k\) to make a new one-time key \(IV||k\), and make the IV public”. You can call this the “IV-Prepend Mode of Operation” for RC4; it was used in a WLAN Security Protocol called “WEP”. Then came the FMS attack that killed this mode of operation, and WEP, and in a sense even RC4 itself because no one wanted to see the next clever idea that would be used to apply the same RC4 key to multiple plaintexts, and that idea’s inevitable catastrophic failure.
The RC4 KSA works by initializing a 256-byte array S where initially S[i]=i, and then performing 256 “swaps” between the values of S[i] and S[j] where the value of i just predictably goes from 0 to 255 and the value of j kind of pseudo-randomly dances around.
Below is the exact code. For clarity, from here on we will denote \(k\) to be the full IV-prepended key that gets fed to the algorithm (so k[0], k[1], k[2] are together the IV, and k[3] and onward is the original secret key). Again, note that the IV is always public and therefore known to the attacker.
#All additions are modulo 256, all key indexes are modulo the key length
#Init: i<-0; j<-0; S <- S[i]=i for all i
for i in range(256):
j += S[i] + K[i]
swap values of S[i] and S[j]
The FMS attack (original paper here) exploited a certain statistical bias in RC4’s KSA and PRGA. As it turns out, if IV[0]=3 and IV[1]=255, the resulting one-time key \(IV||k\) induces the KSA above into a very specific behavior. We will denote IV[2]=X and note that this value is known to the attacker. Let’s see what happens to the permutation S with each iteration of the KSA.
Permutations are given in cycle notation as seen in your favorite undergrad discrete math course — \((xyz)\) means “what was in \(x\) has now moved to \(y\); what was in \(y\) has now moved to \(z\); what was in \(z\) has now moved to \(x\)”. Or in other words S[z]=y, S[y]=x, S[x]=z (note the inverted order!). This notation makes the evolution of the permutation \(S\) easier to follow, using the identity \( (aX) \times (aY) = (aXY) \) (for example, in the second row below: \( (30) \times (31) = (301) \) – applying \((30)\) first and \((31)\) second).
| \(S\) | \(i\) | \(S[i]\) | \(k[i]\) | \(j\) | swap |
|---|---|---|---|---|---|
| \(()\) | \(0\) | \(0\) | \(3\) | \(3\) | \((30)\) |
| \((30)\) | \(1\) | \(1\) | \(255\) | \(3\) | \((31)\) |
| \((301)\) | \(2\) | \(2\) | \(X\) | \(X + 5\) | \((2[X+5])\) |
| \((301)(2[X+5])\) | \(3\) | \(1\) | \(k[3]\) | \(X + k[3] + 6\) | \((3[X+k[3]+6])\) |
| \((301[X+k[3]+6]) (2[X+5])\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) | \(\ldots\) |
Let’s stop and perform a little thought experiment. What if the KSA just stops here, and we immediately invoke the PRGA and obtain the first keystream byte? The PRGA code is below:
#All additions are modulo 256
#init: i<-0, j<-0
while True:
i += 1
j += S[i]
swap values of S[i] and S[j]
output S[S[i]+S[j]]
The first output byte is S[S[1]+S[S[1]]]. But in the current state of S we have S[1]=0 and S[S[1]]=S[0]=3, so the output byte equals S[3] which is 6+X+k[3]. The attacker knows the value of \(X\) and, hopefully, they also know the value of \(6\). So if they can get this output byte, they can solve for k[3], which is an actual byte of the secret key.
That’s it! That’s the attack! All the rest is pesky details, and if you don’t care about them, you can stop reading here. If you do care, we present them below, in increasing order of peskiness.
Pesky detail #1: How is the attacker supposed to get the first byte of the key stream? Isn’t that a secret? — Well, yes and no. Technically it is a secret, but because RC4 is a stream cipher, a known plaintext attack is enough to recover key stream bytes. Specifically for WEP, the first byte of the plaintext was something called a “SNAP header” which almost always had the same known byte value, 0xAA. So, an attacker can just XOR the first ciphertext byte with 0xAA and obtain the first byte of the key stream.
Pesky detail #2: This recovers just one key byte; what about the rest of the key? — We should emphasize that recovering a secret key byte is very bad already and would be enough by itself to throw the cryptographic scheme in the bin. Still, of course being able to recover the whole key and actually crack open the plaintext is more impressive. The authors do in fact demonstrate how to do this in their original paper: for the next byte, the attacker needs IV[0]=4 now (instead of IV[0]=3) and they follow the way the KSA unfolds just like before, making use of the fact that they now know k[3] . Following the state of \(S\) gets complicated, especially when you write it out in general for the j-th key byte so you’re dealing with expressions like IV[0]=3+j, and all these variables inside the current state, and so on. This is why we chose to just show you the case j=0 and hand-wave what happens next (but you are welcome to try the next step with j=1 for yourself).
Pesky detail #3: Wait, in reality the KSA doesn’t just stop like that! — That’s true, it doesn’t. To understand how the attack gets around that, note that for the attack to succeed, it’s enough if the rest of the KSA doesn’t modify S[1], S[0] and S[3]. As long as the randomly-wandering j doesn’t take on the value 0, 1 or 3 during the remaining 253 swaps, the attack will still succeed. This scenario happens with probability \(\left( \frac{253}{256} \right)^{253} \approx 5\%\). You might ask “what use is this attack that succeeds 5% of the time” — well, if you wait for, let’s say, 300 “spicy” IVs and try the attack with each (again recall IVs are public) you can expect the attack to yield the correct key byte about \(300 \times 0.05 = 15\) times, while yielding every other byte at a much lower rate uniformly at random. The candidate key byte that appears more times than the rest is probably the correct one.
Side Channel Attacks
Unfortunately, we cannot use cryptosystems as they exist in abstract math-land. We have to construct them in the physical world, and then have them be used by actual people. This introduces a great number of complexities and implementation details, and often it happens that we examine those details and find the Devil lurking there.

We must note that by considering the real world, we bring into view a great many vectors of attack that no one would call “cryptographic”. This category includes phishing, infostealer malware, and that whole business with “Rubber Hose Cryptanalysis” — a term coined in 1990 by Security Researcher Marcus J. Ranum, who described an attack where “[..] a rubber hose is applied forcefully and frequently to the soles of the feet until the key to the cryptosystem is discovered, a process that can take a surprisingly short time and is quite computationally inexpensive” (see also the relevant xkcd).
While that whole can of worms is definitely out of scope for this text, the same is not true of the narrower set of attacks that abuse the actual details of an implementation. This category of attack was a key ingredient the slew of 2010s Acronym Attacks on TLS (FREAK, POODLE, DROWN, etc. — you can read about those in more detail here). Specifically, we will now explore the narrower still set of attacks that abuse an information leak due to some specific cryptographic implementation. Such an attack is called a side-channel attack.
Timing Attack
Imagine that you are tasked with infiltrating a medieval castle, and a guard is posted at the entrance. The security protocol specification is clear and simple: at the door, you hand over a piece of paper which contains a password. Only people who have handed over the correct password are allowed entry. You have a year to complete your task; let’s say that, realistically, you can walk up to the guard and try to gain entry once a day. If you try every password in order (a brute-force attack), then even for a simple 5-letter password, you will need over 32,000 years to complete the attack, which is well over the time limit.
But suppose the guard is a very slow reader and takes a full 3 seconds to read a single letter. On the first day you walk over to the guard and hand over a piece of paper that says aaaaaaaa. After 3 seconds the guard says “Wrong password, go away”. The next day you approach the guard again and hand over a piece of paper that says baaaaaaa. After 3 seconds the guard sends you away again. The next day you hand over a piece of paper that says caaaaaaa, and again 3 seconds later the guard sends you away. The NEXT day, though, something interesting happens. You hand over a piece of paper that says daaaaaaa, and the guard now takes a full six seconds to send you away.
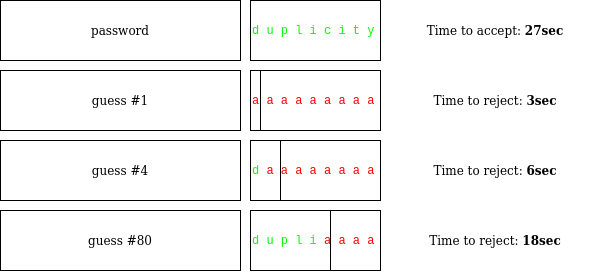
What happened? The guard took three seconds to read the first letter of your submission, but unlike the previous three days, did not immediately become convinced that your password was wrong. They had to check the next letter, which took another three seconds. In other words, just from this delay alone, you conclude that the first letter of your guess was correct — the correct password starts with a d.
So the next day you walk up to the guard again and hand over a piece of paper that says dbaaaaaa, and the guard sends you away after six seconds again. The day after that, you try dcaaaaaa, and again after six seconds you get sent away. Finally, about a month into your attack, you hand over duaaaaaa and the guard takes a full nine seconds to send you away. Clearly, after six seconds of reading the first two letters, they were still not convinced your password was wrong, so they had to spend another three seconds reading the third letter. It follows that u must be the second letter of the correct password.
You keep this up and reveal the next letter of the password and then the next, until finally you uncover the full password, “duplicity”. This takes a total of about 120 days. Mission successful! The weakness was not in the protocol itself, it was in the implementation. The guard’s behavior leaked information on the password via the time required for computation. This is called a timing attack.
The existence of such attacks is the reason that many implementations of cryptographic algorithms take care to use “constant time”, that is, to have computation time not depend on secret input. In this write-up, the “chosen plaintext” blog explains what this entails in practice, and even generalizes the principle to cover other side-channel attacks that monitor e.g. power consumption. The write-up advises “secret-independent resource usage”, where “secret information may only be used in an input to an instruction if that input has no impact on what resources will be used and for how long”.
Portable Instrument for Trace Acquisition (PITA)
As mentioned above, the principle behind timing attacks applies equally well to other system behavior that can be externally monitored, such as power consumption. One example of this is the astounding 2015 paper from Tromer et al. which demonstrates how to steal encryption keys from laptops using a piece of pita bread (rather, a contraption the size of one).
This is a chosen ciphertext attack: the attacker can choose ciphertexts and have them decrypted, with the goal of being able to decrypt all future ciphertexts without this access. Usually this is done by recovering the key, as is the case here. More specifically, this is a “non-adaptive” chosen ciphertext attack, which means that the attacker does not have to invent or modify ciphertexts on the fly depending on how the attack plays out. They can prepare a list of ciphertexts in advance.

This attack targeted implementations of RSA and ElGamal running on a laptop. We won’t go into the full technical details, but the gist is researchers discovered that for numerical values with a certain structure, when multiplying by that value, the decryption algorithm would exhibit some interesting visible behavior (that is, visible to an antenna).
From our earlier description of differential cryptanalysis, you should already have an idea about the immediate danger when the intermediate state of a cryptographic process is subject to an information leak. Sure enough, the researchers crafted certain ciphertexts that they knew would induce values with this structure somewhere along the computation, with the exact value of “somewhere” depending on the key. This allowed them to recover the full key relatively quickly, sometimes using as few as 8 decryptions.
Honorable Mention: SPECTRE
This is not a cryptographic attack, but a proper feat of dark magic, which is too good not to include here. At the time SPECTRE was published, it broke all OS security boundaries and was at first dismissed by some in the semiconductor industry because it seemed too disastrous to be true.

Imagine that your employer maintains a library full of documents, some classified and some not. To read a classified document, you have to present your credentials to the librarian. But the librarian is very short on time, so the moment you even express interest in any documents at all, she sends an errand boy to go fetch them from the back room just in case, even if the credentials will not check out. The errand boy puts any requested documents into the librarian’s Quick Access drawer under the front desk, because clearly these documents are now popular, seeing as you just asked for them, and it’s expected that in five minutes some other person will probably arrive to check them out again.
You turn to the librarian and say, “Hey, go look at the company salary records for me, and if Bob’s salary is higher than mine, I want to borrow War and Peace. Otherwise, I want to borrow Romeo and Juliet.” The errand boy heads out back, looks at the company salary records, finds out that Bob’s salary is twice yours and concludes that you’ll be borrowing War and Peace. On the way back, he discreetly puts War and Peace (and the salary records) into the Quick Access drawer, and reports to the librarian. The librarian adjusts her glasses, looks at you sternly and says, “Excuse me, you’re not getting War and Peace or Romeo or Juliet or anything else. Your request started with ‘look into the company salary records…’ and you lack the proper credentials for that.” So you say “Fine, then I just want to borrow War and Peace.” The librarian immediately pulls it from her Quick Access drawer, and thus answers your question about Bob without meaning to.
Having understood that, you now understand SPECTRE. The librarian is the operating system, the errand boy is the CPU, the Quick Access drawer is the cache and you’re a rogue process with no permissions, trying to read privileged system memory (such as kernel data structures). This is the kind of power that timing attacks possess: direct information leaks where information leaks should definitely not exist. Seeing as these attacks are a concern even in the much harsher context of access control, where the attacker is just not supposed to have access to some information, we hope you can see how potent this kind of attack can be when targeting a cryptographic algorithm, which at least gives the attacker something to work with.
Choice Attacks on RSA
Choose your Crash Course in Public Key Cryptography

RSA works by using a public key \(e\) that is known to everyone and can be used to encrypt a message \(m\) by computing \(m^e\), and a private key \(d\) only known to the key owner, that can be used to decrypt some ciphertext \(m^e\) by computing \( (m^e)^d \) which (by some mathematical dark magic) equals \(m\) again.
You can stop here if you want. This is already enough to understand several attacks on RSA — precomputed table, existential forgery and Bleichenbacher’s attack. Below we try to give a technical explanation of RSA at the level required to understand some other attacks on RSA, such as the Cube Root attack and the Coppersmith method. If you find that this technical explanation tests your patience, feel free to skip all the way through to the next section, and just read about the first three attacks.
In the beginning there were primitive substitution ciphers like the Caesar Cipher and Atbash, which didn’t even involve a key and could be thought of as more of an obfuscation than proper encryption. Then there was the era of increasingly complex substitution ciphers: shift, Vigenère, even the Enigma machines, all of which fell prey to increasingly complex frequency analysis. Finally, there were modern symmetric ciphers: DES, which faded into relative irrelevance over several decades due to ever increasing hardware capabilities, and AES, which is a widely used standard to this day.
At first glance the introduction of modern ciphers seems to have solved the problem of secure communication. Alice and Bob just have to agree on an encryption key, and they’re set. But, then, how do Alice and Bob agree on a key securely if they don’t have a secure channel already? They could meet in person, but that isn’t always practical.
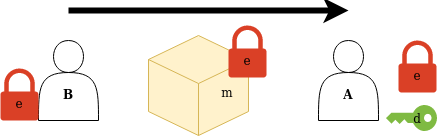
Another idea is that they use spring padlocks: anyone can lock these, but once that’s done, only someone with the matching key can reverse the process and unlock. This allows Bob to send things securely to Alice: Alice buys a set of spring padlock and padlock key, then keeps the padlock key and sends the padlock itself to Bob. Bob takes a message \(m\) and puts it inside a sturdy metal box, then locks the box by squeezing Alice’s padlock, and mails the box to Alice. Alice unlocks the padlock with her padlock key and takes \(m\), confident in the knowledge that no one saw it or tampered with it while in transit.
Now note that Bob could have specifically chosen \(m\) to be an AES encryption key. So, problem solved… sort of, because this still isn’t very practical. The real breakthrough was when we found out that you could build a set of spring padlock and matching key out of math.
To understand how this works, first we have to remind you that you already know modular arithmetic. You use it every day. For example, you start watching a movie at 23:00, and it lasts 3 hours; what hour does the movie end? 02:00. So, \(23 + 3 = 2\). What if you watch the movie 70 times back-to-back? At what hour will you be done? Well, it takes \(3 \times 70 = 210\) hours, which is 8 days and 18 hours. Hour-wise, you’ll be done 18 hours later than when you started, at 17:00. Meaning that we have: \(3 \times 70 = 18\), and \(23 + (3 \times 70) = 23 + 18 = 17\). For these hour calculations, \(24\) is the “wrap around point”, called the modulus. We can pick another modulus if we want. For example, if the modulus is \(5\), then we have \(3 + 4 = 2\).

An important aside that will come into play later is that in modulus-land, performing division is easy. Meaning that if we pick some modulus and ask, “\(7\) times \(x\) is \(80\), what is \(x\)?” there’s a simple algorithm to find the answer (or the several possible answers, or that there is no answer).

The second thing we need to explain is the very simple mathematical concept of a group. A group is made of elements. Just like you can multiply two numbers, in a group you can “op” any two elements. You can also un-op by any element, and there’s a “1” element that does nothing when you op with it. That’s all, that’s what a group is. So, for example, if we look at all the numbers on the number line with the multiplication op, that’s not a group, because you can’t “un-op” (divide) by zero! But the same thing without the zero element is a group. Another famous group is the Rubik’s cube: every move you make, you can immediately undo, if you so like. The “1” element for the Rubik’s cube is just doing nothing.
What is the concept of a “group” good for? It turns out that just from always being able to “un-op” you get some interesting properties. For example, let’s write “\(a\) op \(a\) op \(a\)” as \(a^3\) for short. For the size of the group \(G\), let’s write \(|G|\) for short. It turns out that in a finite group, if you pick some element \(a\), you always have \(a^{|G|} = 1\). For example, in a group of \(5\) elements, “\(a\) op \(a\) op \(a\) op \(a\) op \(a\)” will always be \(1\), no matter what \(a\) you pick. This is due to a result called “Lagrange’s theorem”.
The legend goes that one Passover, Rivest, Shamir & Adelman were sitting around the Seder table and they figured something like this. Suppose you have a group \(G\) and you can somehow tell people how to perform the group “op” without revealing the size of the group, \(|G|\). You pick some element \(g\) and some number \(e\), and announce these to everyone; they are your “padlock”. Now — watch carefully, here comes the magic trick! — you secretly compute some \(d\) with \(ed=1\) modulo \(|G|\). Remember that we said if you know the modulus (in this case, \(|G|\)) then solving such an equation is easy. The resulting \(d\) is now your private padlock key. You keep it close, and don’t give it to anyone.
Now a curious property has emerged where anyone can “encrypt” group elements, but only you can “decrypt” them. How? Let’s take some group element \(a\). Suppose someone computes \(a^e\) (that is: \(a\) op \(a\) op \(a\)… \(e\) times), which they can easily do because \(e\) is public. Figuratively, they have “locked \(a\) in the box, with \(e\) as the padlock”. By using your padlock key \(d\), you can take this \(a^e\) and compute \((a^e)^d\) (that is: \(a^e\) op \(a^e\) op \(a^e\)… \(d\) times). By middle school power laws, this equals \(a^{ed}\).
Here something interesting happens. Remember, \(ed = 1\) modulo \(|G|\). Just by definition of how this whole “modulo” thing works, this literally means we can write \(ed= k|G|+1\), with \(k\) a whole number. Meaning:
$$a^{ed} = a^{k|G| + 1} = \underset{k\text{ times}}{\underbrace{a^{|G|} \times a^{|G|} \times … \times a^{|G|}}} \times a^{1} = \ldots$$
…But we know \(a^{|G|} = 1\) (due to Lagrange’s theorem), so…
$$\ldots = \underset{k\text{ times}}{\underbrace{1 \times 1 \times \ldots \times 1}}\ \times a^{1} = a$$
By raising \(a^e\) to the power of \(d\), you’ve recovered the original \(a\) out of the locked box! And it’s really not clear how someone without access to \(d\) is supposed to accomplish this feat. Computing \(d\) from \(e\) is easy if you have \(|G|\), but if you don’t, then well…
That’s RSA. Of course, there’s still the question of where we can get such a weird group, for which the public knows how to perform the group op, but doesn’t know the group size. It turns out this can be done by choosing two primes \(p\), \(q\) and taking multiplication modulo \(pq\) as the op. That’s still not a group because you have 0 in there and a bunch of other elements that are “kind of like 0” in the sense that you can’t un-op (divide) by them, so you take those elements away and now it’s a group. We won’t go into the details but we’ll note that the final group size is \((p−1)(q−1)\) elements. Suppose you publish \(pq\) (typically called \(n\)), but not \(p\) or \(q\). To perform the group op — that is, multiplication modulo \(n\) — it’s enough to know \(n\), which is public knowledge so anyone can do it easily. But it’s really not clear how someone with no access to \(p\) and \(q\) can recover the group size \((p−1)(q−1)\). This is where you get those pop science claims about how “modern cryptography is built on the difficulty of factoring”. An easy algorithm for breaking numbers into prime factors would break RSA, because anyone could take the public \(n\) and recover the private \(p\),\(q\).
If in the back of your mind you’ve been wondering how come you haven’t heard much about “elliptic curve RSA”, that’s because elliptic curve groups don’t inherently have this exotic property!
Entry Level Attacks on RSA
We’ve noted above that with the typical cryptosystem, once you try and use it in practice, you run into all sorts of snags that aren’t apparent just from looking at the theory. This is five times as true for RSA. Naive, newborn, “textbook” RSA as described above is elegantly beautiful, but also very fragile, and allows a list of attacks that could by themselves take up this entire article. Each of these attacks necessitates a tweak to protect RSA against it. Adding in all these tweaks is how you get grown-up RSA, the one actually implemented in e.g. your web browser.
Let’s start with something simple. RSA as above allows anyone to encrypt values, but only Alice the key owner can decrypt. This means Eve could take the list of all possible group elements, encrypt each one, and construct a precomputed table of all encrypted values and their decrypted counterparts. With this table in hand, Eve can perform decryption just as easily as Alice. To mitigate this, RSA should be used with a block length large enough to make the construction of this table not feasible.
But even when there is a huge number of potential messages, if Eve can predict some values that will be encrypted by the public in practice, she can abuse this to mount an attack. For example if people commonly encrypt one of the 3 messages “ATTACK”, “RETREAT”, or “WAIT FOR ORDERS” for Alice to read, Eve can simply encrypt those three plaintexts herself and again construct a precomputed table for those specific 3 values. From that point on, any time someone encrypts one of those plaintexts for Alice, and Eve sees the encrypted text in transit, Eve will be able to recover the original plaintext immediately by using the table.
To prevent this attack, before being encrypted, messages should be randomized in some way. If we write “WAIT FOR ORDERS” and then add 200 random bytes, then encrypt the result, send the ciphertext to Alice and say “Hey, ignore those last 200 plaintext bytes”, she will have no problem of it; but Eve’s attack as described above will no longer be feasible.
We would be remiss not to mention here something called “existential forgery”. This is more of a Jedi mind trick than a proper attack. In this scenario, Eve first writes down some “signature”. The contents don’t matter; you can imagine it says, “this is definitely a legitimate signature, nothing suspicious here”. Eve then encrypts this “signature” using Alice’s public key and obtains “Alice’s message” which is most likely just a bunch of garbled bytes. Eve then walks up to an unsuspecting Bob and says, “look at this bunch of garbled bytes that Alice wrote, I fear for her mental health”. Bob asks “can you prove Alice wrote that?” and Eve produces the “signature” and theatrically shouts, “Look! This is the decryption of that bunch of garbled bytes! Only Alice has the private key so only she could have computed that. There’s your proof.” This is exactly as idiotic as it sounds, and one way to mitigate it is to have it be common knowledge that Alice will only sign hashes of messages, not plain messages (see above under “birthday attack on digital signatures” for more details about that).
Bleichenbacher’s Attack
The cryptographic doom principle (slightly paraphrased) states: “If a protocol performs any cryptographic operation on a message with a possibly malicious origin, and behaves differently based on the result, this will inevitably lead to doom.” For (a simple) example, in a simple substitution cipher, if the server expects every plaintext message to end with “A”, you can send the ciphertexts “AA”, “AB”, “AC” and so on. For most of these, the server will shout “improper plaintext”, except for one ciphertext. Let’s say it’s “AX”; now you know that X decrypts into A. This generalizes to much more complicated setups than this example: if you control the ciphertext and can get the server to leak information on the resulting plaintext, you can wreak all sorts of mischief. (If you are interested in a more involved exposition of oracle attacks, see our previous write-up.)
Bleichenbacher’s attack targets RSA when used with a certain message scheme called PKCS1, which takes the role of the “properly formed plaintext expected by the server”. A proper PKCS1 message starts with the bytes 00 02, and some RSA implementations respond with different error messages depending on whether the message is “proper” or “improper”.
Even without considering anything about the way RSA works, the doom principle tells us enough to suspect a possible attack here. We control the ciphertext, we can send forged messages to the server, and the server will leak information about the resulting plaintext by telling us whether that plaintext had the proper PKCS1 form or not. The only thing left is to tease out the particulars due to the specific encryption scheme used.
Suppose that we are given a ciphertext c, and would like to know its decryption cd. We can send forged ciphertexts to the server, and it will dutifully tell us for each ciphertext whether its corresponding plaintext is a valid PKCS1 message or not. How do we proceed? What modifications can we make to an RSA ciphertext that will have a predictable, interesting effect on the plaintext?
By middle school power laws, we have for all \(x\) and \(y\):
$$\text{decrypt}(xy) = (xy)^d = x^d y^d = \text{decrypt}(x) \times \text{decrypt}(y)$$
The same holds true for encryption. This is called the “multiplication property” or the “homomorphic property” of RSA.
We can use this property to our advantage. Suppose we multiply \(c\) by some factor of our choice \(m\) (called a “blind”), and send the resulting forged ciphertext \(mc\) to the server for decryption. By the multiplication property, the corresponding plaintext equals \(\text{decrypt}(m) \times \text{decrypt}(c)\). Since the server leaks information regarding this plaintext, and since the decryption of \(c\) is the prize we’re after, this seems like a promising start.
However, we’ve hit a snag: we have no idea what our decrypted blind \( \text{decrypt}(m) = m^d\) actually is. We do know the original blind \(m\) that we picked, but only the server knows \(d\). We can’t do much with an information leak about (total unknown \(\times\) our target). The total unknown gets in the way.
Fortunately, there’s a clever trick to bail us out. The value of \(d\) might be secret, but \(e\) is public. Suppose therefore that we scratch our original plan. After picking the blind \(m\), we write it down and then instead of using it as-is, we encrypt it with the public key, \(e\), and use the result \(m^e\) instead of our original blind \(m\). As we’ve just seen, the server will leak information about (decrypted blind) \(\times\) (original plaintext), but since we sneakily used an encrypted blind to begin with, we instead get an information leak on (decrypted encrypted blind) \(\times\) (original plaintext). The astute among you will note that a decrypted encrypted blind is just a blind, and therefore we now have an information leak on (blind) \(\times\) (original plaintext), which in equation-speak is \( m(c^d)\). Unlike \(m^d\), we do know \(m\); the snag has been unsnagged.
The bottom line is, we pick some random number \(m\) and send \((m^e)c\) to the server. The server attempts to decrypt our ciphertext and, as we’ve just shown, arrives at \(m(c^d)\). If the server actually accepts this resulting plaintext, we obtain valuable information: we now know that \(m(c^d)\) begins with the bytes 00 02. Since we know \(m\), we can use this knowledge to greatly whittle down the pool of possible values for \(c^d\). We then go back and try many more values of \(m\), cross-referencing the resulting constraints on \(c^d\) until there is only one possible value left.
If you took the short version of the crash course on RSA, that’s enough now! You’re free! You can skip the next several sections and go directly to the conclusion. For everyone else, we follow with some attacks on RSA that involve abusing the actual underlying mathematical machinery.
Cube Root Attack
This attack is so ridiculously simple that the method itself can still be stated without any regard for the mathematical structure of RSA. Encryption is performed by computing \(m^e\) for some message \(m\), so just… take the \(e\)-th root? Where’s the problem? (The attack takes its name from the popular choice of value \(e=3\)).
Well, while in high school math it’s easy to take the cube root of a number, it is not always so easy when doing modular arithmetic. What is the cube root of 13 modulo 30? The answer “2.3513…” does not work, as we only use whole numbers in modular arithmetic. On the other hand, what is the cube root of 1,000 modulo 7,000,000? It’s 10, obviously, and the same if the modulus is 8,000,000 or for that matter 1,001. As long as \(N > 1000\), then \(10^3\) modulo \(N\) is still 1,000 — the modulus just never comes into it. In other words, if the entire operation of computing \(m^e\) can take place without ever exceeding the original modulus and “wrapping around”, that’s when the attack works.
Therefore, one way to mitigate the cube root attack is to ensure that no “small” messages are ever encrypted. One way to do it that immediately springs to mind is to simply add some large “padding” to every outgoing message — that is, instead of encrypting \(m\), we encrypt \(m+a\) where \(a\) is some fixed, public number that’s large modulo \(N\).
Unfortunately, by doing this we run into two more attacks.
Broadcast attack
Suppose you want to send the same message \(m\) to several people (Alice, Bob and Charlie) in encrypted form, and each of them has their own RSA public key using \(e=3\). Alice has the modulus \(N_1\), Bob has \(N_2\) and Charlie has \(N_3\). To perform the encryption, you compute \(m^3\) mod \(N_1\); \(m^3\) mod \(N_2\); \(m^3\) mod \(N_3\); and send these to Alice, Bob, and Charlie, respectively. These encrypted messages are now public knowledge.
Surprisingly, Eve can abuse this scenario to mount what is basically a revived cube root attack, even assuming the plaintext \(m\) is padded. To do this, she makes use of a mathematical fact known as the “Chinese Remainder Theorem”. It says that if 3 moduli (in this case \(N_1\), \(N_2\), \(N_3\)) are coprime, then for any number \(r\) you can look at \(r\) mod \(N_1\), \(r\) mod \(N_2\), and \(r\) mod \(N_3\), then use those values to compute \(r\) mod \(N_1 \times N_2 \times N_3\). In this case, Eve is able to compute \(m^3\) mod \(N_1 \times N_2 \times N_3\). Because of the way RSA works, we must have \(m < N_1\), \(m < N_2\), \(m < N_3\). Multiplying those equations together, we get \(m^3 < N_1 \times N_2 \times N_3 \). So, with this huge new modulus \(N_1 \times N_2 \times N_3\), the cube root attack is possible again.
Note that because with the “fixed public padding” we mentioned earlier a message \(m\) always maps to the same padded message \(m+a\), this padding does not prevent the attack.
Related Message Attacks
Consider the converse scenario: Instead of sending the same message to several recipients, you’re sending different messages to the same recipient, but the messages are somehow related. For example, suppose we have two messages \(m_1\) and \(m_2 = m_1 +1\). So now Eve has access to the two ciphertexts \(c_1 = m_1^3\) and \(c_2=m_2^3 = (m_1+1)^3\). Eve then simply computes:
$$\frac{c_{2} + 2c_{1} – 1}{c_{2} – c_{1} + 2} = m_{1}$$
Maybe you want to write it out, expanding the expressions for \(c_1\) and \(c_2\), collecting like terms and so on; we’ll be here when you’re done. One way or another, it seems cube roots are difficult when doing modular arithmetic, but this difficulty cannot survive the existence of two equations and some algebra.
This example is from a 1996 paper by Coppersmith et al, who then proceed to consider the more general case where \(m_2 = \alpha m_1 + \beta\), and give the somewhat unwieldy explicit expression that Eve has to compute in terms of \(\alpha\) and \(\beta\):
$$\frac{\beta\left( c_{2} + 2\alpha^{3}c_{1} – \beta^{3} \right)}{\alpha\left( c_{2} – \alpha^{3}c_{1} + 2\beta^{3} \right)}$$
What IS that?! Should I be scared?
No. These kinds of strange, unwieldy expressions are typical of mathematical situations like this, where some object or another is guaranteed to exist via some algorithm, and then the algorithm is actually carried out and all the messy numbers collide. For comparison look at the following polynomial: \(f(x) = \frac{1}{24}x^{4} – \frac{1}{12}x^{3} + \frac{11}{24}x^{2} + \frac{7}{12}x + 1\). This is just a polynomial f with f(x) = 2x for x = 0, 1, 2, 3, 4, which is guaranteed to exist via a process called “Lagrange interpolation” (basically the fact that you can pass a line through any two points, generalized to more points and a higher degree polynomial). Someone familiar with what’s happening under the hood doesn’t scream “aaah, \(\frac{7}{12}\), where did that come from”; they just say “right, right, a Lagrange interpolation, very cute”.
Coppersmith et al then go on to consider the use of an arbitrary exponent \(e\) instead of the fixed \(e=3\) in the above example. They give an eye-straining formula for the expression Eve has to compute for \(e=5\), then mention in passing that a formula should always be possible for whatever \(e\) you pick, but the formula and the process for determining it both get very unwieldy for larger values of \(e\).
Instead, they go another route. They note that for the given exponent \(e\), the message \(m_1\) is a root (solution) of two polynomials: \(z^e – c_1 = 0\) and \(\alpha z + \beta – c_2 = 0 \). Also, in all probability, \(m_1\) is the only value with this property. Somewhat surprisingly, it’s an easy mathematical operation to extract the sole common root of two polynomials (surprisingly, it’s done with the exact same algorithm we mentioned before for solving \(ax = 1\) modulo \(N\), the extended Euclidean algorithm). This easily generalizes to more ciphertexts, more complex known polynomial relations between the plaintexts, and so on.
Coppersmith’s method
The original “cube root attack” simply says that finding the solution \(x_0\) of a polynomial \(x^n – c = 0\) modulo \(N\) is easy under “cube root conditions”: that is, when the modulus is large enough, or more precisely when \(|x_0^n| < N\). It turns out that having these favorable “cube root conditions” is even more powerful. Even if instead of \(x^n – c\) we are challenged with any degree-\(n\) polynomial \(f\), we can still extract \(x_0\).
This feat can be accomplished using something called “Coppersmith’s Method”. Like a lot of powerful strategies, it begins with a bit of wishful thinking: if only “cube root conditions” still applied when evaluating the actual \(f(x_0)\) — that is, if only we had \(|f(x_0)| < N\), then we’d be done. The reason is that when computing \(f(x_0)\) no “modular wrap around” would occur. We’d just be solving \(f(x)=0\) in regular number-land, without worrying about modular arithmetic. Your calculator can do that; it’s basically the same logic as the original cube root attack.
Of course, the snag is that the “cube root conditions” we stated earlier — \(|x_0^n| < N\) — don’t guarantee that. Sure, \(n\) (the degree of \(f\)) is guaranteed to be small, but maybe the polynomial \(f\) is actually \(x^3 + 17N\) or something, and now what do we do? Just the term \(17N\) leaves us stuck with the modular wrap-around that we need to get rid of so that we can throw our calculator at the problem. Fortunately, we know of a working algorithm for “a polynomial \(f\) has a root \(x_0\); find \(f\) with small coefficients that still has that root \(x_0\)”, though it’s best we don’t dive here into the technical details of how that algebraic feat is pulled off (the process involves using a lattice-theoretic algorithm called an “LLL basis reduction”).
The immediate use of this method is in situations where recovering \(m\) with a root attack would be straightforward, except that due to some padding scheme or another, we are looking at a ciphertext of the form e.g. \(m^7 + 5m^2 + 1\). But the really interesting thing is that Coppersmith’s method is relevant even for more advanced attacks. Note that all attacks on RSA we’ve discussed so far have abused the padding being deterministic. This seems to suggest that to make RSA more resilient, random padding should be used. However, it turns out that in some situations, attacks using Coppersmith’s method can even be extended to apply to related messages that were each padded with random bytes. This involves constructing polynomials in two variables, and computing something called a “resultant”; for anyone interested in this avenue of attack, we recommend section 2 of this paper.
Conclusion
We began by surveying some “classic flavor” modern cryptanalysis methods, including the meet-in-the-middle attack that rendered 2DES dead on arrival; applications of the birthday paradox for attacking digital signatures and block ciphers; then finally discussed what “information leak” means in a cryptographic context and talked about the broad subject of attacks abusing statistical biases in cryptosystems, including differential cryptanalysis and the milestone FMS attack that cast WEP out of polite company.
We then discussed side channel attacks — including timing attacks, analogous power consumption monitoring attacks, including the curious case of the PITA attack, which stole encryption keys using a literal peace of leavened bread — as well as the SPECTRE vulnerability, which was not a cryptographic attack in the strict sense, but was such an astounding demonstration of the power of timing attacks that we had to mention it.
Finally, we turned to attacks on public-key cryptography, specifically focusing on RSA. We described some basic attacks that did not involve too much mathematics and were due to the very structure of RSA as a cryptosystem where anyone can encrypt — including a precomputed table and existential forgery, and even the more complex Bleichenbacher’s attack, which did require RSA’s homomorphic property. We then moved on to some attacks that directly abused the way that RSA’s mathematical elegance is also a source of weakness: The basic Cube Root attack, the broadcast attack, related message attacks and finally Coppersmith’s method and a taste of its capabilities.
There’s no denying that the sheer volume and complexity of attacks that have gained relevance during the modern era of cryptography can get very overwhelming, very quickly. “Who is meeting whom in the middle? WEP died because of… statistics? What do you mean ‘differential’ cryptanalysis, what is this, calculus?”. This write-up does not cover, and cannot hope to cover, the full range and depth of these attacks. Even for RSA alone, the attacks described above are just a small fraction of a large volume of documented attacks; for those with an interest in RSA specifically, we recommend Boneh’s twenty years of attacks on the RSA cryptosystem. Some other interesting attacks that did not find room here include Wiener’s Attack and its out-of-the-blue use of an esoteric number-theoretic tool called “continued fractions”; The basic Pohlig-Hellman attack on DHKE and its follow-ups; and fault attacks, where flipping a single bit in a cryptographic operation can destroy the whole scheme.
Those of you who’d read this article’s spiritual predecessor were first treated to explanations of some simpler maneuvers — brute-force, interpolation, downgrade, cross-protocol and precomputation attacks — then had a taste of what a more modern attack looks like with the oracle attack, including its many practical applications (POODLE, FREAK, DROWN, and the rest). Whether you enjoyed both articles or read this one as a stand-alone, we hope that we’ve managed to shed some light on the fascinating landscape of cryptographic attacks, and render it a little bit more legible and welcoming.





