The Illusion of Privacy: Geolocation Risks in Modern Dating Apps

Key takeaways

• Dating apps often use location data, to show users nearby and their distances. However, openly sharing distances can lead to security issues. Techniques like trilateration allow attackers to determine user coordinates using distance information.
• Despite safety measures, the Hornet dating app (a popular gay dating app with over 10 million downloads) had vulnerabilities, allowing precise location determination, even if users disabled the display of their distances. In reproducible experiments, we achieved location accuracy within 10 meters.
• The recent changes applied by the Hornet developers to mitigate the risks reduced the location accuracy to 50 meters.

Introduction

Dating apps traditionally utilize location data, offering the opportunity to connect with people nearby, and enhancing the chances of real-life meetings. Some apps can also display the distance of the user to other users. This feature is quite useful for coordinating meetups, indicating whether a potential match is just a short distance away or a kilometer apart.

However, openly sharing your distance with other users can create serious security issues. The risks become apparent when you consider the potential misuse by a curious individual armed with advanced knowledge of techniques like trilateration. Trilateration lets you determine target coordinates by knowing the coordinates of several points and the distance from them to the target. In some cases, it’s sufficient to have precise distances to two points and an approximate distance to a third.

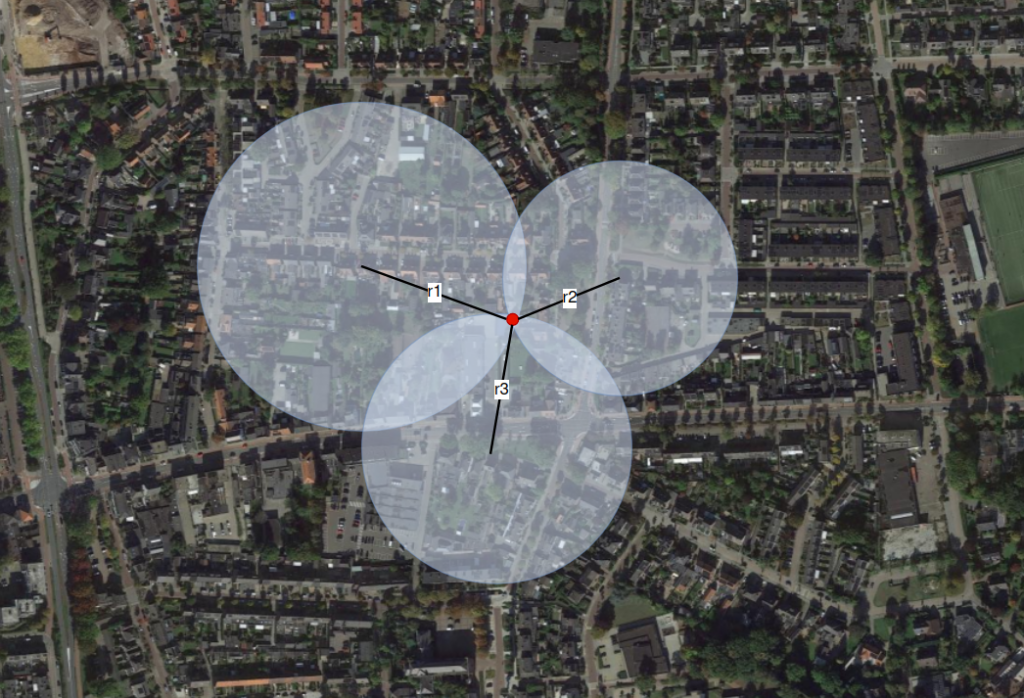
Figure 1 – Use of distances for determining the unknown position coordinates of a point of interest.

Imagine the app disclosing your exact location to any user. Faced with such a breach of privacy, you might be tempted to deny the app access to your geolocation data. This concern is even more pronounced on gay dating apps, where vulnerability is heightened by the reality that LGBTQ+ rights are still violated in some parts of the world. In these regions, it’s not just a choice but a crucial necessity to keep personal information, such as geolocation, private.

Previous publications by researchers on this topic prompted developers to take measures to ensure user safety and prevent geolocation leakage, such as:

• Rounding of geographical coordinates.
• Rounding and randomly altering the distance to users in search results.
• The option to hide the distance.

We analyzed two popular gay dating applications with 10M+ downloads, mentioned in previous studies, to find out how safe they are for users nowadays. Both applications allow users to disable the display of their distance.

The first of the dating apps we looked at transmits coordinates encoded as a 12-digit geohash, where the map is divided into rectangles of 37×18 centimeters. We analyzed the traffic and discovered that before geohashing, the geographical coordinates are rounded to 3 decimal places. This reduces the theoretically possible accuracy of determining the user’s location to a rectangle whose longer side measures about 110 meters, which is quite a large area.

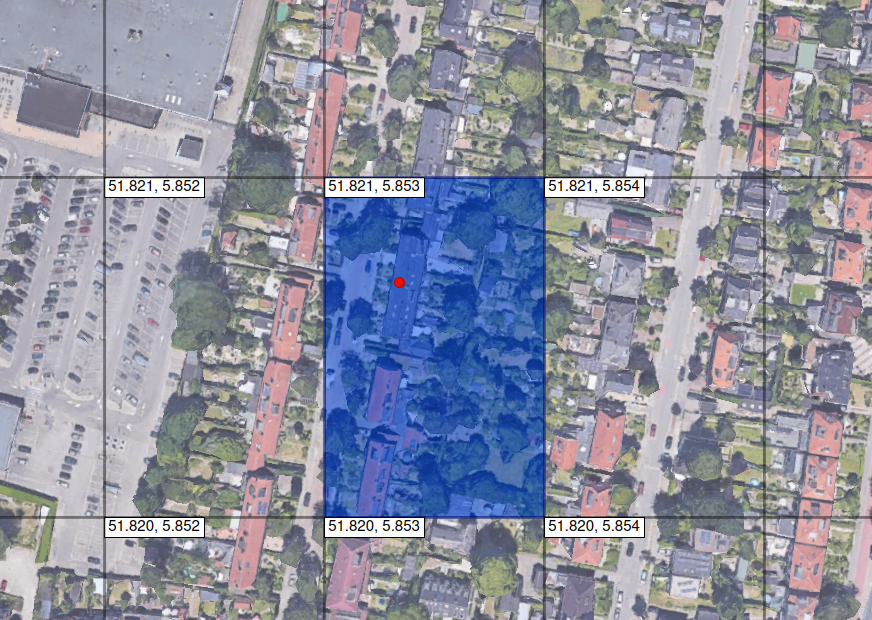
Figure 2 – Reducing the location accuracy when rounding coordinates to three decimal places.

While the first application we studied reduces location accuracy on the client side, the second one, named Hornet, sends precise coordinates to the server. Hornet’s creators are aware of the potential risks of user positioning, as mentioned on their website. At the same time, they claim to protect user locations by randomizing the distance displayed in the application, making it, in their opinion, impossible to determine the exact location. They also announced a feature that allows users to completely disable the distance display:

The news media has been full of stories about the vulnerabilities of other gay social apps. On some of our competitors, it is possible for other users to calculate your position. That poses a potential risk to people living in countries where being gay is not okay.
At Hornet, we have always been aware of this potential security risk, and we took steps long ago to protect our users’ locations. Hornet randomly alters your distance as it is displayed in the app. By doing so, it would be impossible for anyone else to find your exact location. We think this is the best compromise between usefulness and security for our users.
We also offer our users the ability to deactivate distance altogether on their profile.

At the time of our research, the measures taken by Hornet were insufficient to protect user coordinates, allowing for the determination of user locations with very high accuracy.

Following the responsible disclosure process, we attempted to contact the Hornet team and provide them with the results of our research. Just before publication, we reexamined the Hornet application. Despite not receiving a response to our inquiry, we can confirm that the developers have already taken necessary measures to significantly reduce the accuracy of users’ coordinate determination.

Methodology for determining distance

As mentioned earlier, Hornet lets you disable the display of your distance to other users. Therefore, to conduct trilateration, it is first necessary to learn how to determine the distance to the target.

In this and similar applications, users in the search results are sorted in ascending order of distance. If we find two users in the search results who allow the display of their distance, and the target user is located between them in the search results, we can determine the approximate distance to the target user as an average value of two known distances:

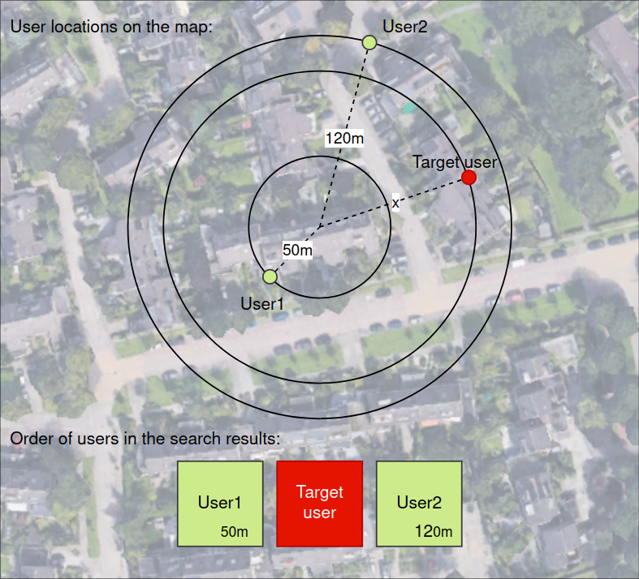
Figure 3 – Estimating the approximate distance to the user based on known distances to neighbors.

However, the presence of users near the target is not a necessary condition. To determine the distance to the user, we need to register an additional account, the coordinates of which we can control. In the next simple example, we demonstrate how we can determine the distance using an additional account. We then show how we can determine the distance with specified precision using an additional account.

Let’s introduce the notations:

• Main – The main account, relative to which we will determine the distance.
• Secondary – An additional account whose position we can control.
• Target – The account of the target user whose coordinates we want to determine.

Let’s assume that Target and Main are located in the same city or an area with a diameter of 100 km.

1. In the first step, we divide the range from 0 to 100 km in half and position the Secondary account relative to the Main account at a distance of 50 km.
2. We request the list of users from the dating app server.
3. If the first user in the search results is the Target, it means that this user is closer to us and is in the first part of the range, and vice versa.
4. Choose the range where the Target is located and divide it in half, positioning the Secondary in the middle of the selected range.
5. Repeat from Step 2 until we obtain the distance with the required precision.

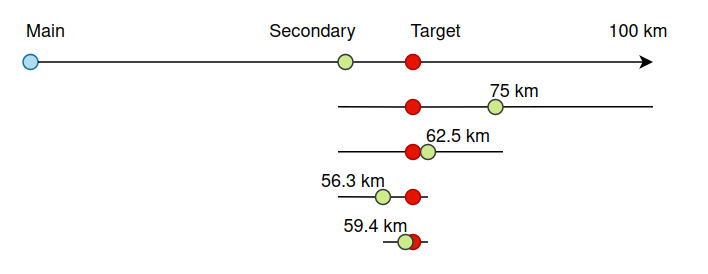
Figure 4 – Technique for determining the distance to the user using the positioning of an auxiliary account.

We want to note that only after the idea came up to us, we found a similar approach described in another study conducted several years ago.

This may indicate that the described technique could have been in use all this time, including by malicious actors.

Experiment

When we attempted to implement the methodology described above in practice, we encountered several peculiarities in the Hornet application.

First, if a user did not deactivate the display of distance for their account, this distance is transmitted to other users with an accuracy of up to 10 meters. However, when we fixed the coordinates of Main and Target and requested the user list multiple times, we found that the application returns a different distance from Main to Target each time:

Figure 5 – Hornet randomizes distances in the search results.

This proves that Hornet indeed randomly alters the distance to users on the server side.

In addition, the distance provided by the server may not even correspond to the order of accounts in the search results:

Figure 6 – The distance to the users provided by the application does not correspond to their order.

This implies that even if the display of distance was not deactivated, the accuracy of this data is very low and cannot be used to determine the exact location.

The second peculiarity is that if the difference in distances to two users becomes less than a threshold value (in experiments, this value was estimated to be approximately 50 meters), it is not guaranteed that they will follow in the correct order in the search results. We positioned the Main, Secondary, and Target accounts on a straight line, fixing the longitude, and started moving Secondary towards Target, calculating the distance each time based on the known coordinates. At a certain point, the Target user started appearing in the list before the Secondary user, even though the distance to Secondary was shorter:

Figure 7 – The real distance to the users does not correspond to their order.

If the users’ locations do not change, their incorrect sequence in the search results persists. When we faced this issue for the first time, it seemed to us that we would not be able to determine the location with an accuracy of better than 50 meters, just as in the case of the first application.

In addition, while analyzing the results of the first measurement, we found that some of them failed. This was because users can be randomly removed from the results even if they are nearby.

However, to solve this issue, it is sufficient to request the list of users multiple times until both the Target and Secondary appear in the search results simultaneously. We also noticed that the more recently a user was online, the higher the probability that they would appear in the results. Therefore, for accurate results it’s better to perform all manipulations when the user is online or was just online recently. This also ensures the relevance of the obtained data.

We found out that there is an API request for notifying the server that the user is online. For our test purposes, we used this API request to ensure that the user is always present in the list of nearby users returned by the server.

We then conducted 1500 distance measurements between random points located at a distance of 1 to 2 km from each other. We used the distance estimation method described above with 10 steps.

In the following image, you can see the distance measurement errors distribution graph:

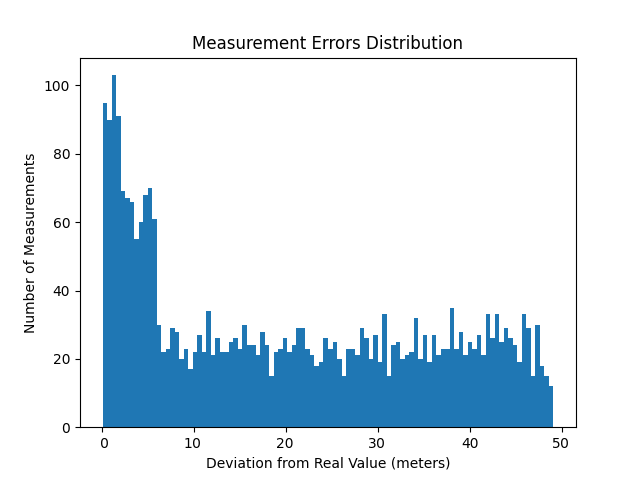
Figure 8 – Distance measurement errors distribution.

The minimum distance estimation error appeared to be less than 0.5 meters, and the maximum is 49 meters. The graph clearly shows that the server randomizes the order of users if the distance between them is less than 50 meters. Additionally, we observe that in the range of 6 to 50 meters, errors are distributed almost uniformly. However, to our surprise, we discovered two peaks within the 0 to 6 meters range. Measurements falling within this range constituted approximately 30 percent of the total.

It is worth noting that the results obtained indicate that in using this technique with high probability we can determine distances with an accuracy of better than 6 meters. By increasing the number of measurements, we can further improve the location accuracy.

Trilateration methodology

For trilateration, we can independently position the accounts under our control. Therefore, when choosing the second and third reference points, to simplify the further calculations, we decided to keep one of the coordinates constant and only change the other.

We used a two-step trilateration: we first performed trilateration using two reference points to obtain two possible candidate locations (intersection points of the circles). Then, we used the distance information from the third reference point to select the correct solution.

As an example, let’s place the reference points (M1, M2) on the same longitude. Next, using the methodology for determining the distance to the point described earlier, we estimate two distances from the reference points to the target point:

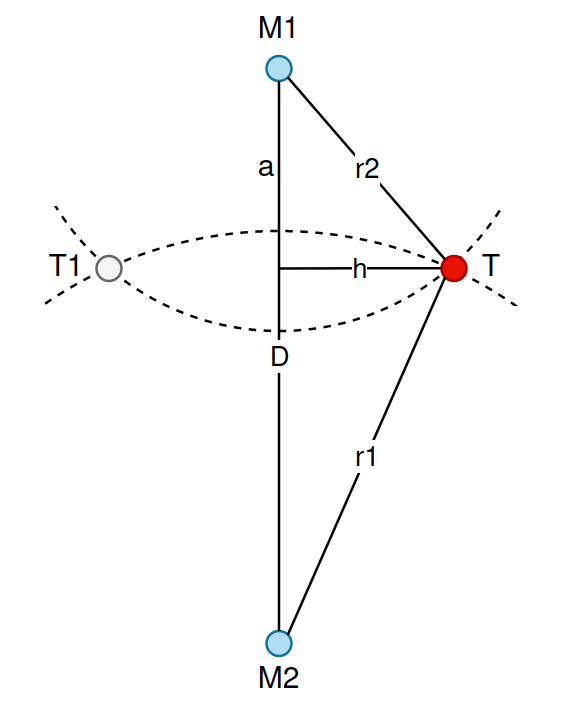
Figure 9 – The first step of trilateration.

By calculating the values of “a” and “h” using the Pythagorean theorem, we obtain two possible coordinates of the target point:

T0 = (M1.latitude - a, M1.longitude + h)
T1 = (M1.latitude - a, M1.longitude – h)

We then repeat the same process for the third point M3 to choose one of the points T0 and T1:

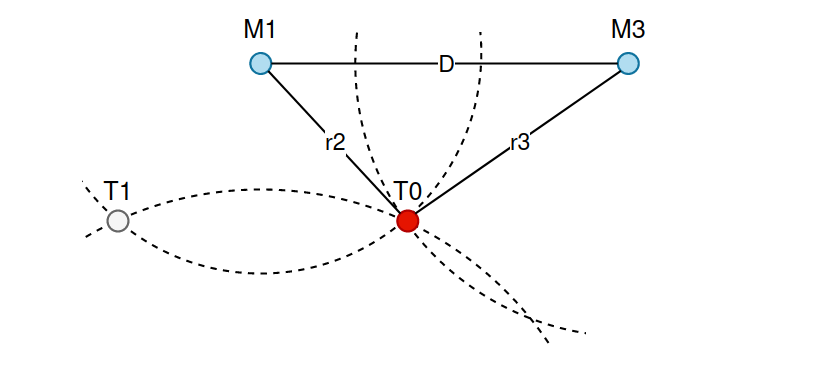
Figure 10 – The second step of trilateration.

Experiment

Let’s assume that we know the area where the target account is located, with a diameter of 10 km. For example, this could be a small town. Around this area, we randomly generated 30 sets of reference points in a ring with an inner radius of 5 km and an outer radius of 10 km:

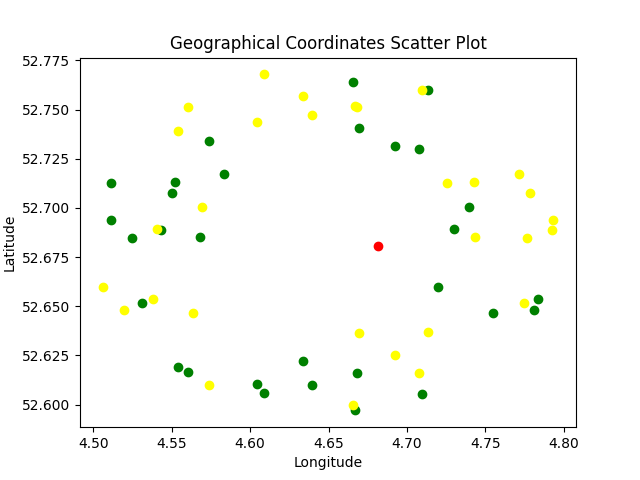
Figure 11 – Location of reference points used for trilateration.

The red point represents the target, while the yellow and green points represent the first and the second reference points. The third reference points for each trilateration were dynamically selected and are not shown on the chart.

Based on the fact that the maximum distance from reference points to the target is 15 km, we used the distance estimation method with 10 steps to determine the distance, providing us with a maximum accuracy of 15 000 m / 2¹⁰ ≈ 15 m.

As a result of trilateration for each group of reference points, we obtained the following set of possible coordinates for the target point:

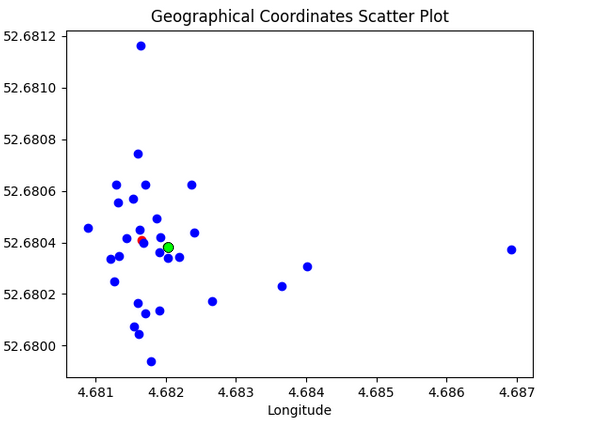
Figure 12 – Trilateration results.

The maximum error in geolocation was 350 meters, and the minimum was only 2 meters. We calculated the mean value of latitude and longitude for all points. The distance between the mean value (the point is marked in green in the image above) and the target point appeared to be 24 meters.

We see that most of the points are concentrated in a small area, except for several points whose coordinates were determined with a large error.

Let’s plot the cumulative distribution function for the distance between the calculated points and the target:

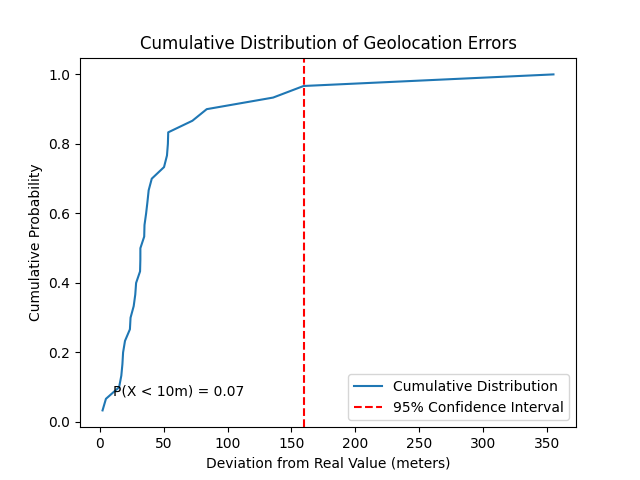
Figure 13 – Cumulative distribution of geolocation errors.

We can see that with a 95% probability, the geolocation accuracy is better than 200 meters. Additionally, by calculating the mean value, we were already able to estimate the coordinates of the target point with an error of only 24 meters.

Improving geolocation accuracy

Now let’s try to improve the accuracy of geolocation. As we can already determine the approximate location, let’s assume that we have identified a region with a radius of 400 meters where the target is located.

For the next experiment, we generated 300 pairs of reference points in a ring with an inner radius of 1 km and an outer radius of 2 km around the area with a radius of 400 meters, where the target is presumed to be. We chose pairs of reference points in such a way that when keeping one of the coordinates constant, they were located in opposite segments of the ring. The third reference point was chosen dynamically.

To determine the distance from a reference point to the target point, we used the distance estimation method with 10 steps of approaching the target. Based on the fact that the maximum distance from reference points to the target is 2 km, this provides us with a maximum accuracy of geolocation of 3 000 m / 2¹⁰ ≈ 3 m.

After conducting trilaterations, we got the following result:

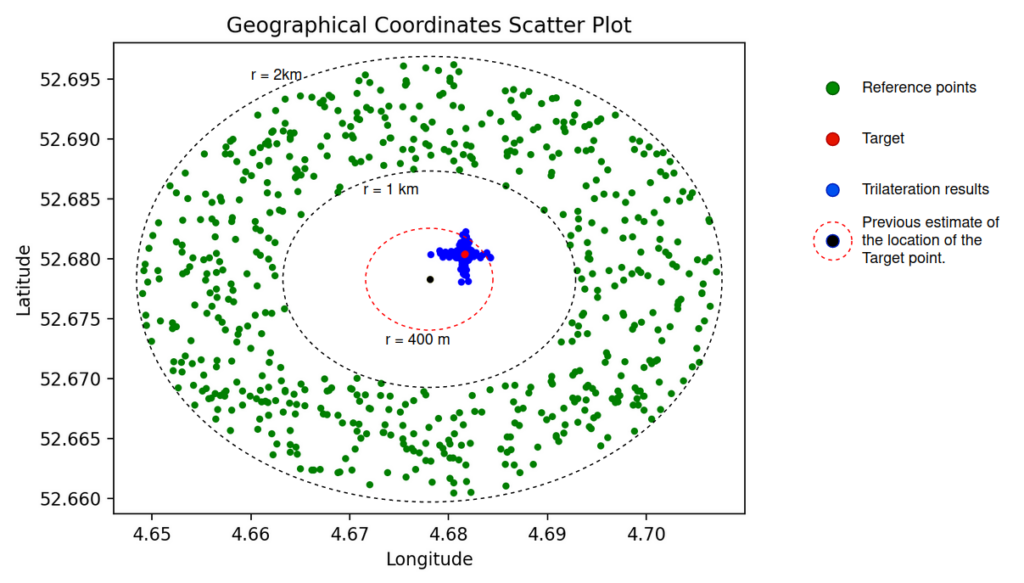
Figure 14 – Reference points and trilateration results.

As in the previous experiment, most of the resulting points are concentrated in a small area; the rest of the points with a larger scatter formed a shape resembling a “+” sign. This arrangement of points is related to the rule we used when selecting sets of reference points, changing only one of the coordinates.

It’s also worth noting that the spread of trilateration results at this stage depends on the distance between the previous estimate of the location (the center of the circle within which we generated reference points) and the actual location of the target point.

In the next figure, we colored the trilateration results with a large deviation from the target in orange and the corresponding reference points in red.

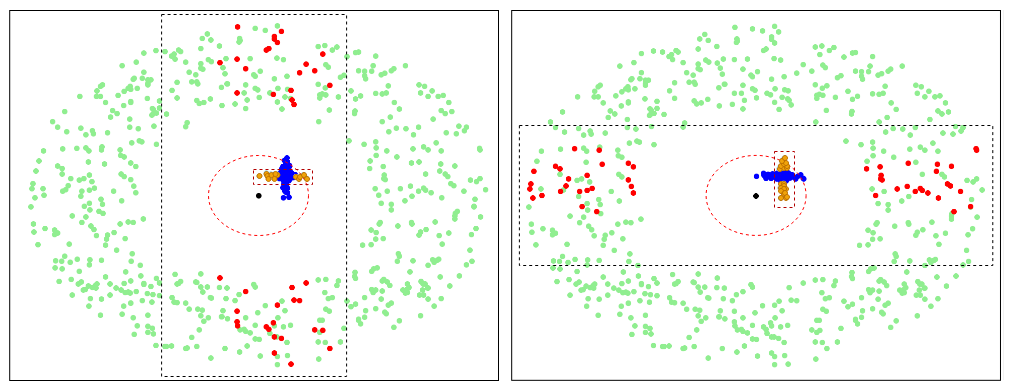
Figure 15 – Trilateration results with a large deviation from the target and the corresponding reference points.

From the figure above, we see that the pairs of reference points that gave the largest trilateration error have a small deviation from the target point along one of the coordinates. Therefore, such reference points can only be used to estimate one of the target coordinates – latitude or longitude. If we want to reduce the number of measurements and, respectively, requests to the application server, we should further exclude such reference points.

Therefore, we removed all reference points whose distance along any axis to the center was less than 800 meters (twice the radius of the previous target location estimate) and obtained the corresponding trilateration results.

We should also emphasize that with such a configuration of reference points, when conducting trilateration, it is sufficient to measure distances from only two points. After that, we obtain two intersections of circles that are far apart from each other. As a solution, it is enough to choose the one that is closer to the previous estimate of the target’s location. If both points are more than 400 meters away from the previous estimate of the target’s location, these points should be discarded. This helps us to eliminate potential errors.

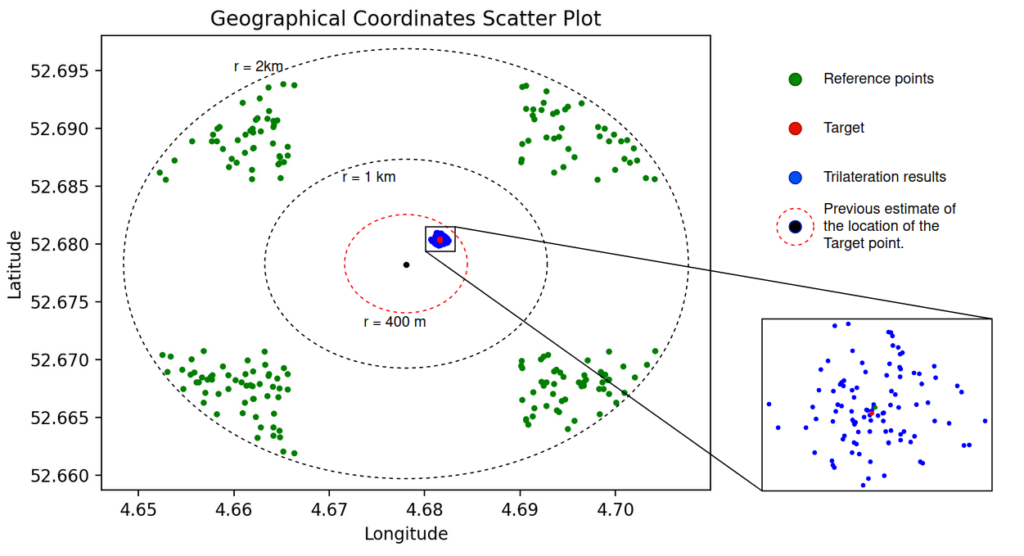
Figure 16 – Filtered reference points and the corresponding trilateration results.

For the results, we also plotted the cumulative distribution function for the distance between the calculated points and the target.

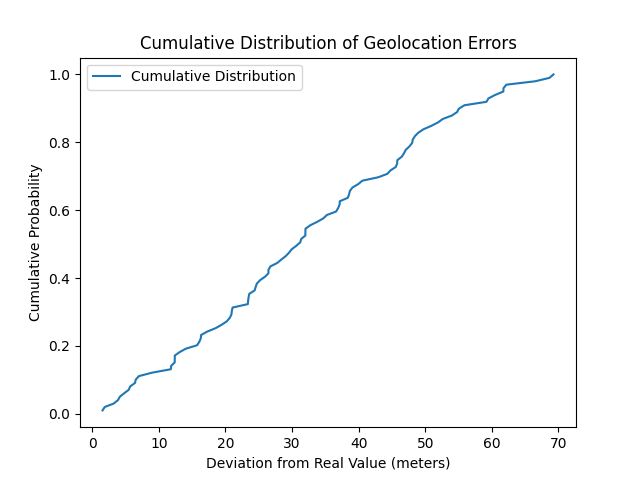
Figure 17 – Cumulative distribution of geolocation errors.

The distances from the points obtained through trilateration to the target point are distributed almost uniformly with a minimum of 1.5 meters, and a maximum of 70 meters.

As in the previous experiment, we also calculated the average latitude and longitude for the results. The resulting average point was less than 5 meters away from the target:

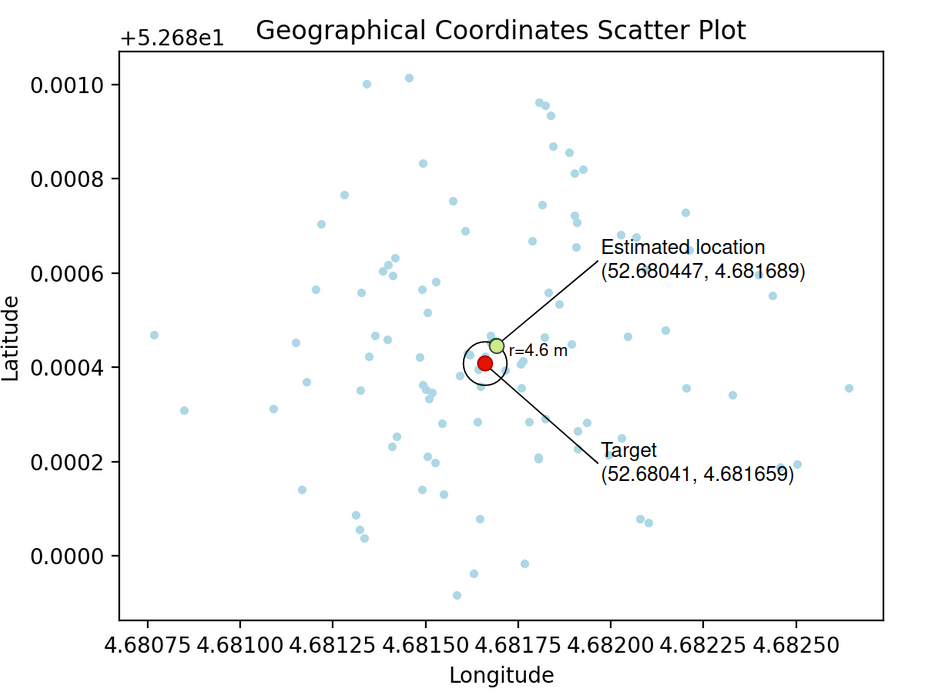
Figure 18 – The final location estimate has an error of less than 5 meters.

We therefore show that despite the randomization of the order of users in the search results, by conducting a large number of measurements, we can determine the user’s location with very high accuracy.

Experimental Replication and Robustness Analysis

To confirm the reliability of our results and assess the average accuracy in determining geolocation, we replicated the previous experiment across various target points and different numbers of reference points. Omitting the initial step of approximating locations, we introduced a random offset to each target’s coordinates, ensuring the final point fell within a 200-meter radius of the original.

For each target point, we utilized the algorithm described earlier to estimate location, involving the averaging of coordinates from multiple trilaterations. Subsequently, we calculated geolocation errors in meters for each target, repeating these calculations with 10, 25, and 50 sets of reference points. The resulting graph illustrates cumulative distribution functions for each of the three sets of results.

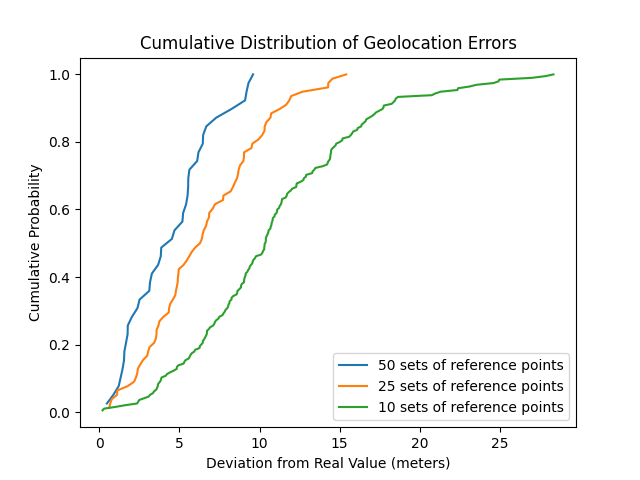
Figure 19 – Cumulative distribution of geolocation errors for 10, 25, and 50 sets of reference points.

From the graph, we can observe that the accuracy of distance estimation improves as the number of reference points increases. When using 50 sets of reference points, we achieved distance estimates with an error of less than 10 meters in 100% of cases:

Number of reference point sets	Max. error, meters	Average error, meters
10	28.3	10.9
25	15.4	6.6
50	9.6	4.5

We also conducted several experiments using 100 sets of reference points. The average geolocation error was about 3 meters. However, measurements for so many reference points take a lot of time. For our experiments in determining the distance, we manipulated the coordinates of only two accounts, and the whole process took quite a lot of time. However, it should be noted that a motivated attacker could create a larger number of accounts, for example, a pair for each reference point. In this case, measuring distance from any number of reference points takes only a couple of seconds.

Conclusion

In the realm of dating applications, exposing user geolocation poses significant risks to privacy. Despite developers’ efforts to enhance security measures, our experiments revealed potential vulnerabilities in the Hornet dating application that has over 10 million downloads. The developed distance estimation methodology, combined with trilateration using a large number of reference points, demonstrated a very high accuracy in determining user locations.

In replicable experiments, we managed to estimate the user’s location with an accuracy ranging from less than a meter to 10 meters. In most cases, such precision allows for pinpointing a user’s place of residence or even distinguishing them among others on the street. In addition, by increasing the number of reference points, a motivated attacker could achieve even better accuracy and determine the geolocation within seconds. Turning off the distance display in the app does not guarantee your location will not be leaked. As we showed, the demonstrated method of determining location works in this scenario as well.

Just before publication, we conducted another examination of the application. As a result, we managed to achieve a level of coordinate accuracy within 50 meters. Increasing the number of reference points does not provide any improvement.

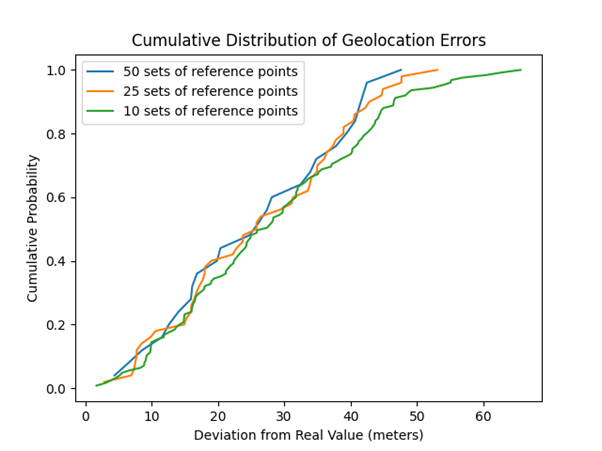
Figure 20 – Cumulative distribution of geolocation errors for 10, 25, and 50 sets of reference points after the vulnerability was fixed.

Compared to the previous accuracy of 10 meters, we can conclude that the developers have taken the necessary measures to protect user locations. However, it should be noted that a motivated attacker can still determine approximate coordinates.

CPR strongly advises users to be vigilant about the permissions they grant to apps and to stay informed about the potential risks and best practices for protecting privacy and security when dealing with geolocation data. By disabling location services, users can prevent apps from tracking their whereabouts and gathering information about their movements. This measure can effectively safeguard user privacy and thwart the sharing of personal data with external entities.