The Cat and Mouse Game: Exploiting Statistical Weaknesses in Human Interaction Anti-Evasions

Executive Summary

• We describe, in very general terms, how we were able to evade detection by taking advantage of statistical anomalies in the human interaction modules of several sandbox solutions.
• We provide an alternative algorithm for simulated mouse human interaction, including its specifications, parameters, source code, and several visual demonstrations.

Why We Care about Sandbox Emulation

As a discipline, information security involves a vast web of entry vectors, mitigations, and counter-mitigations. Among these, one of the most impactful points of conflict between attackers and defenders is what happens when binaries are subjected to sandbox emulation. Purely static analysis has been understood to be a game that attackers win, and defenders lose: code can be obfuscated (“packed”, “crypted”, “virtualized”, take your pick), forcing any analysis to first run it in some way in order to understand it. If you can tell anything at all about a binary’s functionality at face value, it’s due to its author’s lack of effort, not their lack of means.

The same is far from true about sandbox emulation. Countermeasures to sandbox emulations do exist, but each comes with its own baggage, disadvantages, and chance of outright failure. No one-click silver bullet has popularly emerged in the attacker arsenal to just trivialize sandboxes. Some attackers may mistakenly believe they can ‘solve’ sandbox emulation by compiling the al-khaser test suite into their binary and refusing to run if a test fails, but unlike packing, which is a one-way operation, a test suite like this can be flipped around and used as a shield: anyone operating a sandbox can verify that their sandbox passes all the tests. In this way, paradoxically, by publicizing numerous sandbox evasions, projects like al-khaser have significantly cut down the maneuvering space available to attackers.

As a result of all this, the sandbox is one of the focal points where malicious campaigns sink or swim. Binaries that will just execute obvious malicious functionality in a sandbox are, in some fundamental sense, naked and ripe for detection, and so attackers are naturally pressured to add sandbox evasions. The moment they do, we’ve flipped the script on them: now they have to worry about false negatives and false positives. A failed evasion or a falsely triggered evasion both result in the attack chain being cut short. Depending on the attacker’s motivation, this directly equals lost money, lost power, or lost prestige.

Looking One Step Ahead

A natural question to ask is, “Who wins this game in the long run?” That is, if sandboxes and evasions continue to get better, is the natural end result of this process the uber-sandbox that will force binaries to expose all their latent malicious behavior or the uber-evasion that can allow malware to run only when advantageous to attackers? We won’t fully explore this question here, as its scope is huge and involves some notions that we would rather not help find their way to the attacker TTP mainstream (as Lovecraft cautioned, “Do not call up that which you cannot put down”). But we can reasonably discuss some of the next moves attackers might make as long as it’s feasible to get ahead of them.

Observing the way many evasions work as seen in (e.g.) the al-khaser test suite and taking it at face value can lead to a mistaken mental model where ‘evasions’ must result from simple glitches that can be fixed, or otherwise from naive responses by the sandbox to a query about something: some file, some registry key, a disk drive size, some other artifact. One might complacently reason that sandboxes simply need to ‘fix all the glitches and patch all the query results’, and that sandbox hardening is in this way reduced to going through a gigantic check list and is effectively a solved problem. Unfortunately, this approach falls apart in cases where satisfying the query requires, in a strong sense, some intrinsic resource that the sandbox does not have access to.

One example of such a scenario is all evasions having to do with ‘human interaction’. A human is not a simple TRUE result of a call to IsHumanPresent(). Humans have behaviors, tendencies, resources, and capabilities. Until such time that every sandbox has a dedicated AI convinced that it is human and going on about its day-to-day routine in a way indistinguishable from one, this is a difficult and, we argue, under-explored frontier in the sandbox evasion space.

In this article, we first outline an example of such an evasion that bypasses several sandboxes, then provide an implemented mitigation.

Extremely Vague Outline of How the Evasion Works

Evasions based on mouse movements are not new. For example, certain strains of malware from the early 2020s would periodically sample the mouse position and wait for the xor of the X and Y positions to reach a certain value. This was an implicit condition on the number of different values the cursor position would take; it defeated some naive mouse movement emulation algorithms that picked a new random position for the mouse every second or so. This, and some slightly more advanced examples, prompted off-the-shelf sandbox solutions to introduce hardening in the form of less obviously auto-generated mouse movements. One particularly popular movement model used for this purpose is the random walk. Whenever some predetermined amount of time passes, the cursor is moved in some chosen direction by some distance, chosen by a process that has at least some random element.

It is really not our intention here for this to be a copy-paste-able widget or even a guide for successfully evading sandboxes. So we will not quite give the specifics here, but we will say that in many cases, implementations of random walks are vulnerable to a statistical attack. We created a proof-of-concept binary that evaded detection by several off-the-shelf sandboxes but would reliably trigger whenever we let a human naturally move the cursor for a while using a mouse.

Having verified that this is possible, we set out to design an algorithm for simulated mouse movement that will resist this attack (and, hopefully, this kind of attack in general; a short discussion on this issue follows the technical exposition).

Detailed Implementation of the Counter-Evasion

Top Level Summary

The simulated mouse movement algorithm is comprised of the following loop:

1. Wait \(\text{wait_baseline}\) milliseconds, multiplied by the output of an exponential distribution with a mean parameter \(\mu_{\text{wait}}\).
2. Choose the next “target” mouse position \(v_{\text{next}}\) from a Gaussian centered on the current mouse position \(v_{\text{cur}}\), with the coordinates independent and the standard deviation \(\sigma_x\) equal to screen width multiplied by a motility parameter \(m\), with \(0 \leq m \leq \frac{1}{2}\) (and similarly for \(\sigma_y\); if this lands outside the screen boundaries, just pick again.)
3. Pick the length of time used to travel from \(v_{\text{cur}}\) to \(v_{\text{next}}\) by sampling from an exponential distribution with a mean \(\mu_{\text{move}}\). Scale the result to the distance \(|v_{\text{next}}-v_{\text{cur}}|\).
4. Chart a “path prototype” \(\varphi: [0,1] \rightarrow [0,1]^2\) which will set the rate of advancement from \(v_{\text{cur}}\) to \(v_{\text{next}}\). The axis-wise components of \(\varphi\) are each generated separately, by averaging \(\text{wave_count}\) random ‘waves’. Each ‘wave’ is a sine function with a frequency picked uniformly from 0 to \(\text{max_freq}\) and a random shift picked uniformly from \([0,\tau]\) (for the uninitiated, \(\tau = 2\pi\)). The sum of these waves is adjusted so that \(f(0)=0\) and \(f(1)=1\).
5. Each \(\text{interval}\), update the mouse cursor position along the planned path, until it reaches  \(v_{\text{next}}\).
6. Set \(v_{\text{cur}}=v_{\text{next}}\) and repeat.

The code corresponding to this top level behavior is below.

def generate_movement(t: timedelta) -> List[Coor]:
    output_len = int(floor((t.total_seconds() * TIME.MS_IN_S) / TIME.INTERVAL))
    result : List[Coor] = []
    cur_pos : Coor = gauss_step_from(
        [SCR.WIDTH//2,SCR.HEIGHT//2],
        [SCR.WIDTH,SCR.HEIGHT]
    )
    while len(result) < output_len:
        
        next_pos = gauss_step_from(cur_pos,[SCR.WIDTH,SCR.HEIGHT])
        mov_time = pick_movement_time(cur_pos,next_pos)
        mov_steps = time_to_steps(mov_time)
        path = gen_path(cur_pos,next_pos,mov_steps)
        result += path
        
        
        wait_time = timedelta(milliseconds=np.random.exponential(WAIT.EXP_DIST_MEAN)*WAIT.GLOBAL_COEF)
        wait_steps = time_to_steps(wait_time)
        result += [result[-1]]*wait_steps

        cur_pos = next_pos
    
    result = result[:output_len]
    return result

The entire code is available in Appendix A.

We will now explain each of these steps in a bit more detail.

Waiting

We model “user wants to move the cursor to a new location” events as the output of a Poisson distribution. This distribution can be considered as modeling the throughput of an event pipeline where incoming events occur independently of each other (such as the calls in a call center). This is probably not the best possible approximation to human behavior. Still, it is a better approximation than having the delay between one mouse movement and the next be a fixed interval or picking it uniformly.

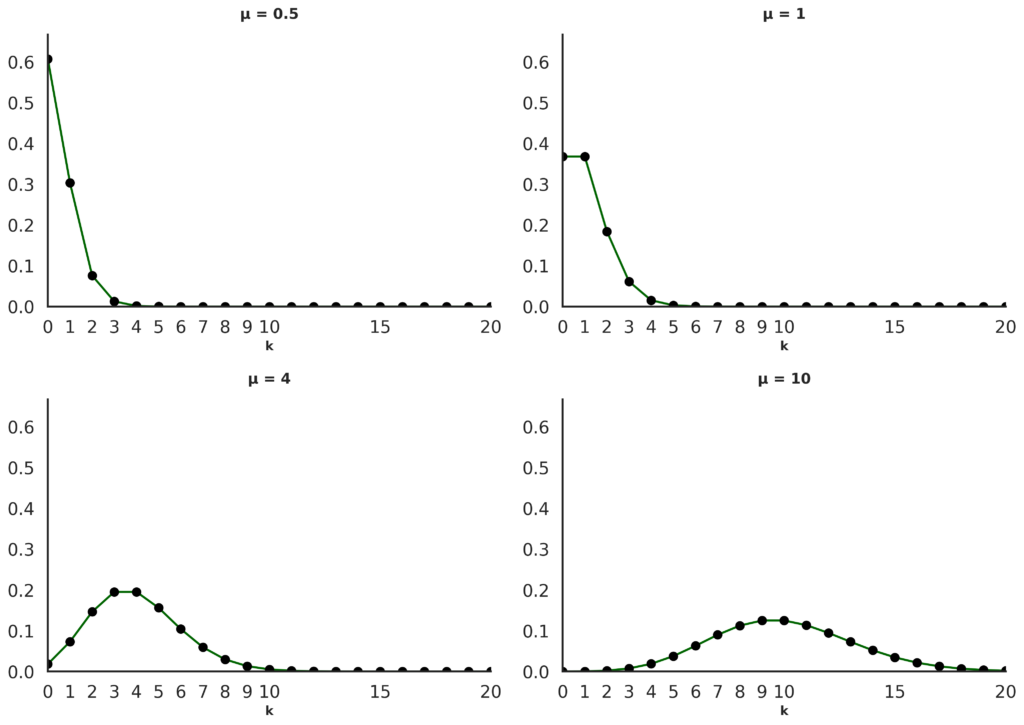
When implementing the simulated mouse movement in practice, the value we care about specifically is the amount of time to delay the next movement. The Poisson distribution equivalently models a process where the time from one event to the next is distributed according to the exponential distribution.

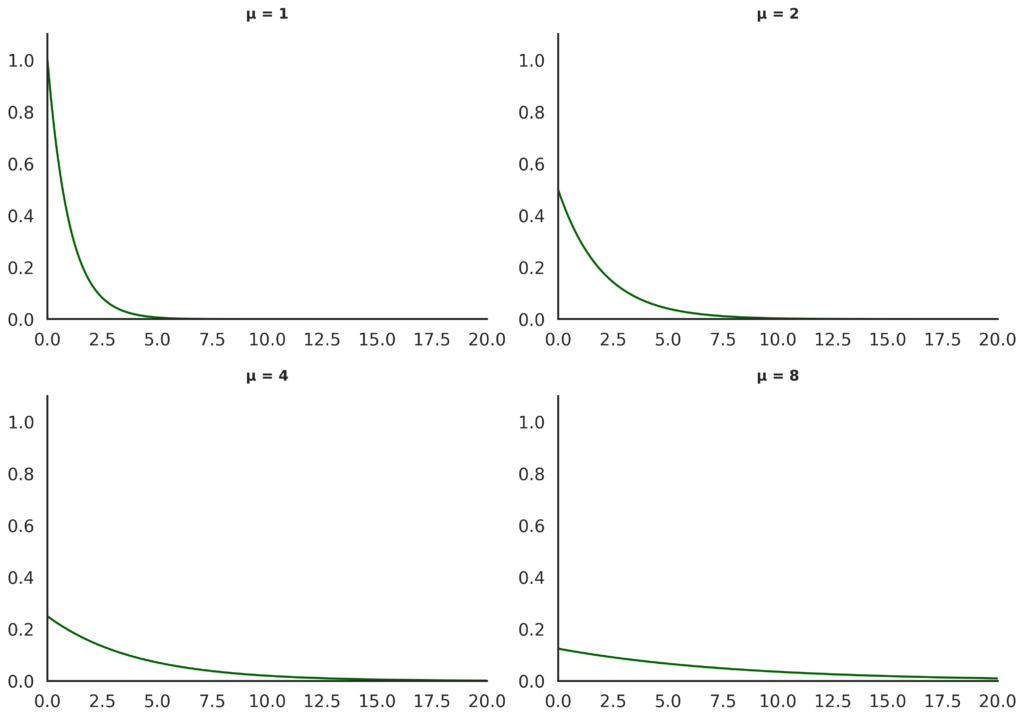
To help visualize what this means about the frequency of events, we include below an animation of incoming events distributed this way (each event represented by a bright white light). The delay between one event and the next is the sample of an exponential distribution with mean \(\mu\), multiplied by a \(\text{time_unit}\) of 1 second.

Setting Next Cursor Destination

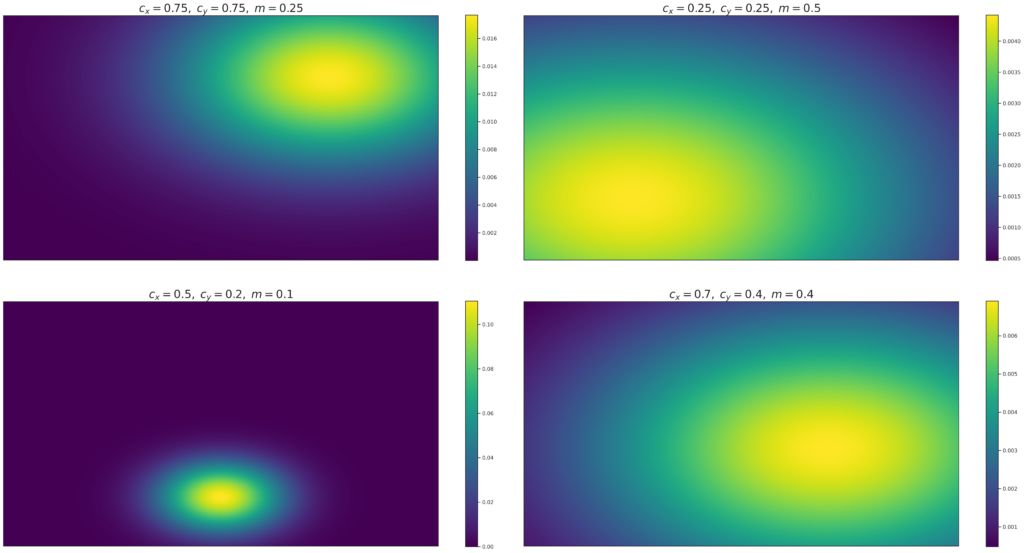
The entire mouse movement, in general, is composed of “segments” that each have a start point and end point. These are not straight lines (perhaps the visualizations in the next sections will help clarify that), but their generation is based on a set starting point and ending point. When generating a new segment, the starting point is the cursor’s current location, and the ending point is sampled from a two-dimensional Gaussian (normal distribution) centered at the current location. The standard deviation along each axis is taken to be mL where m is a “motility parameter” \(0 \leq m \leq \frac{1}{2}\) and L is the total pixel size of that axis (so for an 1920×1080 screen, \(L_x = 1920\) and \(L_y = 1080\)). Below, we include some heat map visualizations for several initial locations on the screen and values of \(m\), for a 16:9 aspect ratio. \(c_x\) and \(c_y\) are the Gaussian mean coordinates normalized to the range \([0,1]\).

Charting the Path Prototype

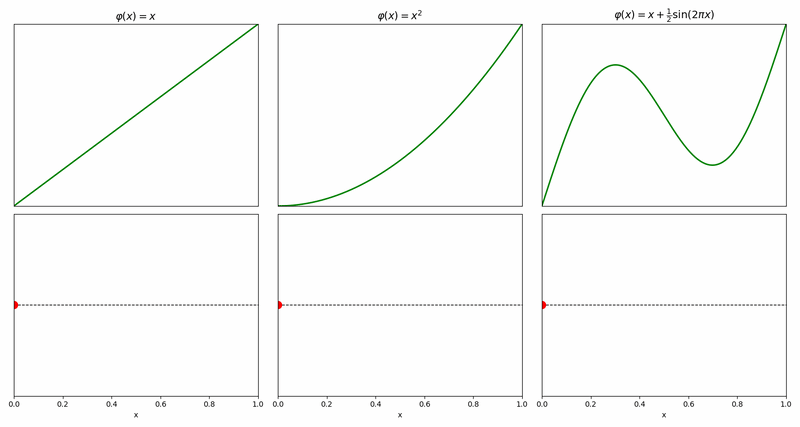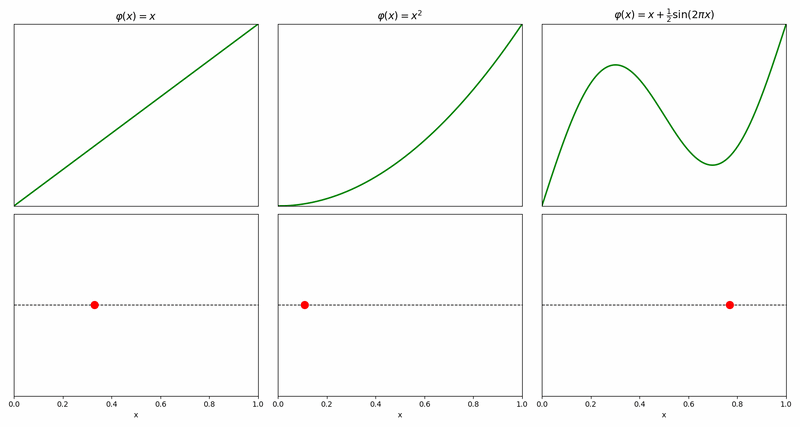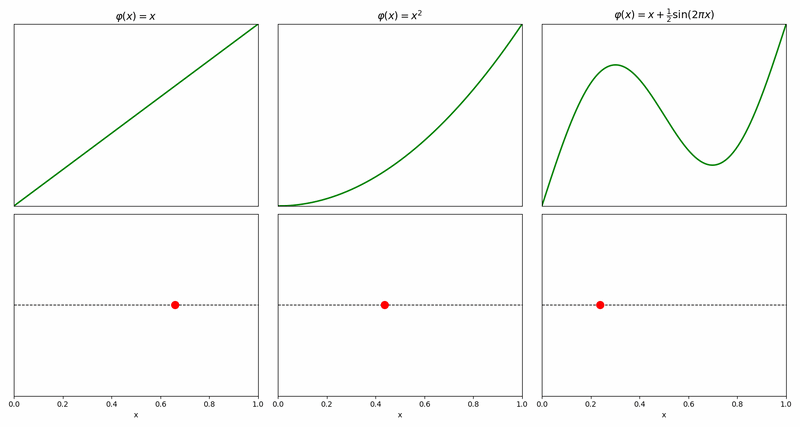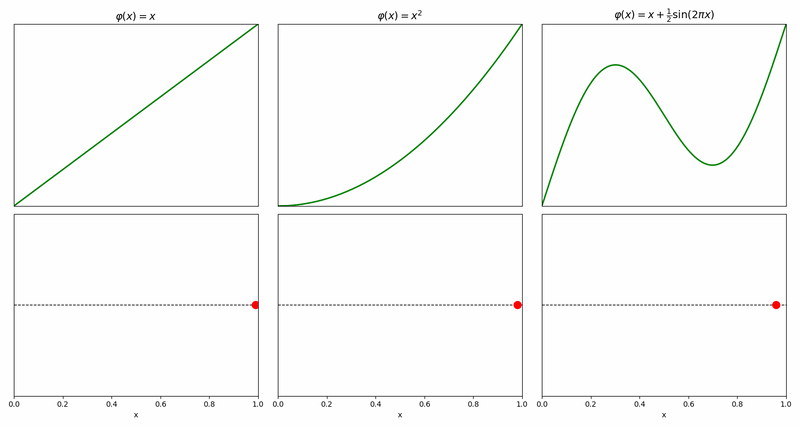
To properly tackle this part, we first introduce the notion of a path prototype. This is probably easier to visualize in one coordinate. Suppose we want to move from \(x=20\) to \(x=80\) during some unit of time. A “prototype” for this movement is a function \(\varphi: [0,1] \rightarrow [0,1]\) that maps “the portion of allotted time that has elapsed” to “the portion of the path we have traveled”. More concretely, the output value of \(\varphi\) is naturally interpreted as a linear combination of the source point and the destination point: so in this example, if \(\varphi(0.5) = \frac{1}{6}\) this implies that when half the travel time has elapsed, the cursor has moved to \(x=30\), having traveled only 10 units out of the 60 required for the whole journey. For obvious reasons we require that a well-formed prototype should have \(\varphi(0)=0\) and \(\varphi(1)=1\).

The simplest prototype is \(\varphi(x)=x\) which implies that the cursor moves from the source to the destination at a constant rate, but other prototypes are possible – some of them not even monotonously increasing, like the example on the right.

Composing two prototypes, one per coordinate, naturally gives an analogous 2d prototype for moving from \((0,0)\) to \((1,1)\).

To generate prototypes that have some variety, we can begin by looking at “periodic noise” of the form \(f(x) = \sin(n \tau x + \phi)\), which has two parameters: \(n\) (frequency) and \(\phi\) (phase). We can choose a parameter \(\text{wave_count}\) and pick this many random noise functions, with each \(\phi\) picked uniformly from \([0,\tau]\) and each \(n\) picked uniformly from 1 to some parameter \(\text{max_freq}\) (our experience has been that letting \(\text{max_freq}\) exceed 5 leads to unstable, jittery results).

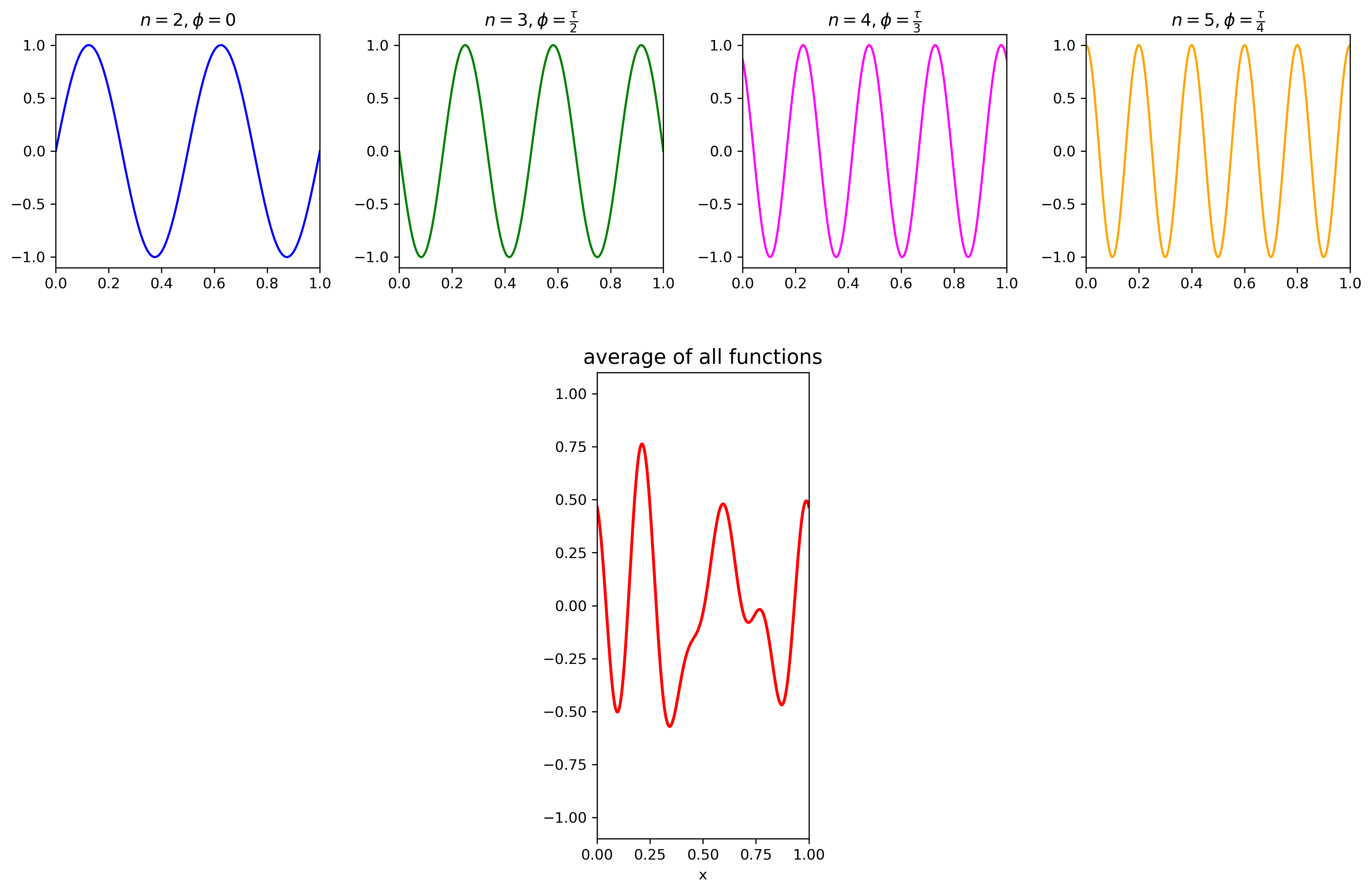
It’s not immediately clear how to get a prototype from this “composite noise” (let’s denote it \(h\)), as it doesn’t have \(h(0)=0\) and \(h(1)=1\), and its values can span the whole range \(-1 \leq h(x) \leq 1\) (because it is the average of many sine waves with this property). To solve this, first of all instead of \(h\) we can use \(\tilde h = \frac{h(x) + 1}{2}\) (which has the desired range, \(0 \leq \tilde h (x) \leq 1\) for \(0 \leq x \leq 1\)). Then, we can take a pointwise linear combination of \(\tilde h\) and \(f(x)=x\). Meaning, we can define \(\varphi(x) = (1-\psi(x))x + \psi(x) \tilde h (x)\), where \(\psi\) is some suitable “combining” function that has \(\psi(0) = \psi(1) = 0\), with \(0 \leq \psi(x) \leq 1\) for all \(0 \leq x \leq 1\) (you might want to algebraically follow what happens to \(\varphi\) when \(x=0\) and when \(x=1\), or just be convinced by the below diagrams). A convenient choice is \(\psi(x) = 4(x-x^2)\), which for the above combined noise gives the following prototype \(\varphi\):

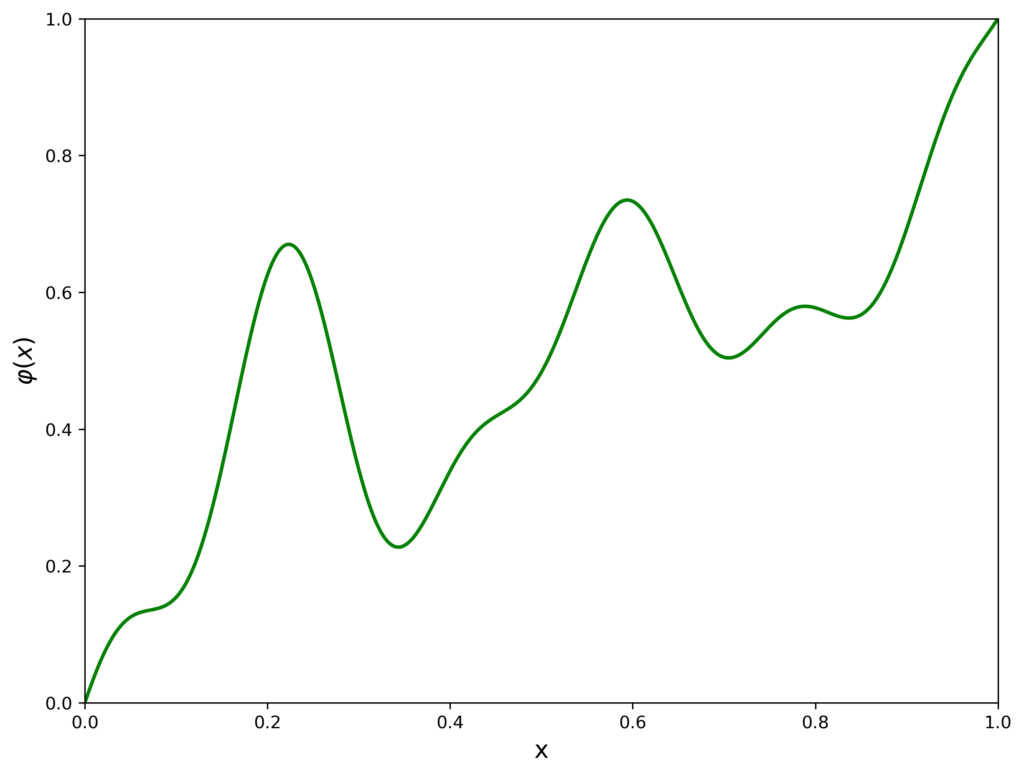
The logic described above is implemented using the following code.

def gen_path_proto_1d() -> Prototype:
    wave = lambda n,shift: lambda x: sin(n*tau*x+shift)
    freqs = [random.choice(range(1,PROTO.MAX_FREQ+1)) for _ in range(PROTO.NUM_WAVES)]
    profile = {f:np.random.uniform()*tau for f in freqs}
    h = lambda x: sum([wave(f,s)(x) for (f,s) in profile.items()])/len(profile)
    psi = lambda x: 4*(x-x**2)
    f = lambda x: x*(1-psi(x))+((h(x)+1)/2)*psi(x)
    return f

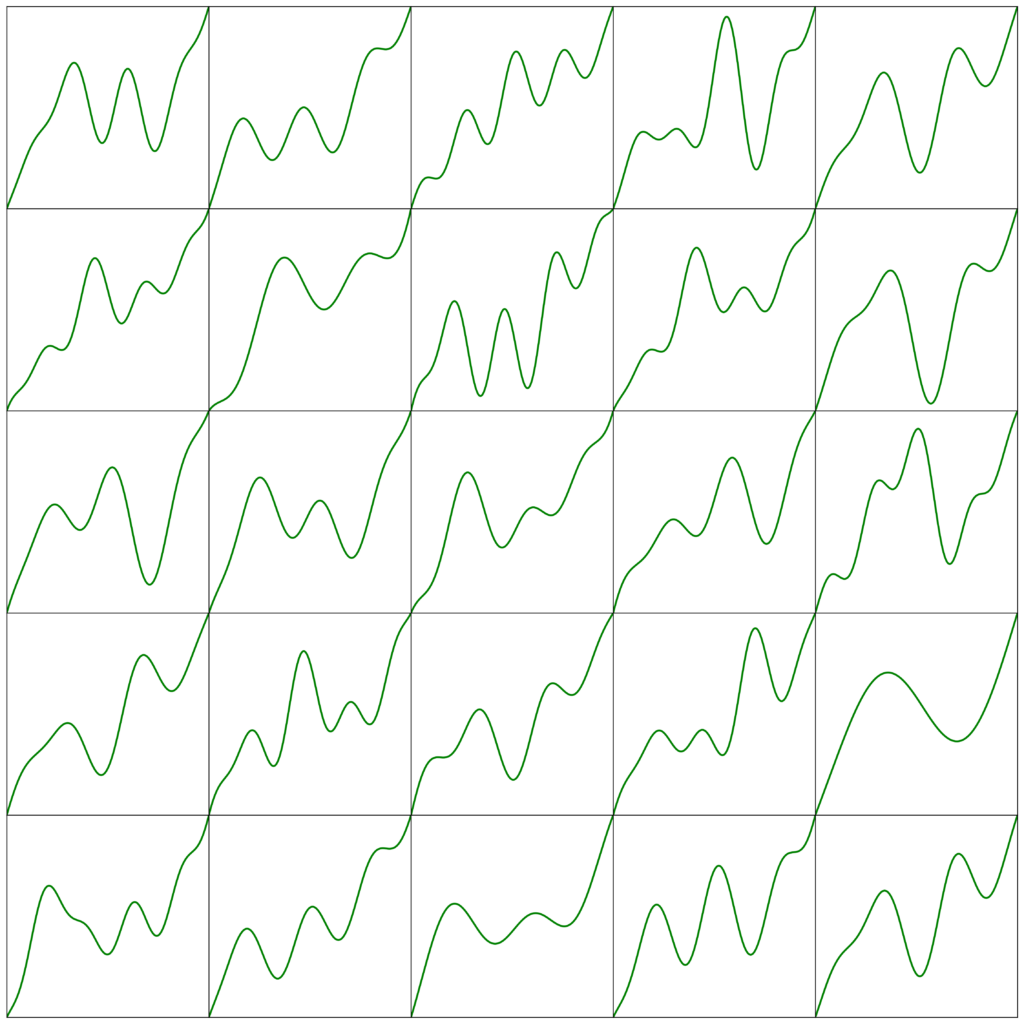
Below is a collection of 25 randomly generated different prototypes using the above process.

Charting the Actual Path

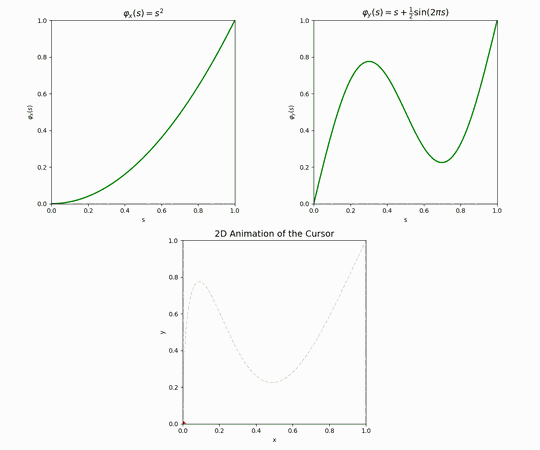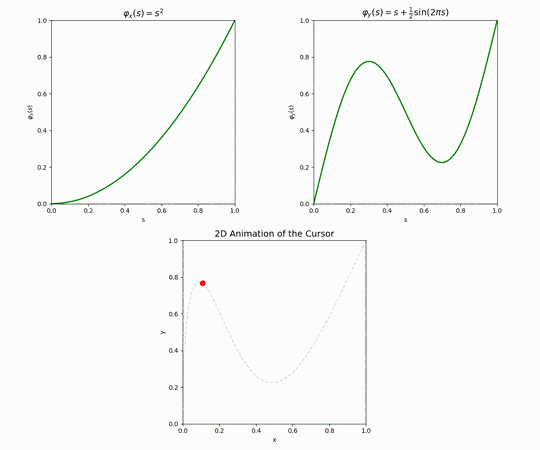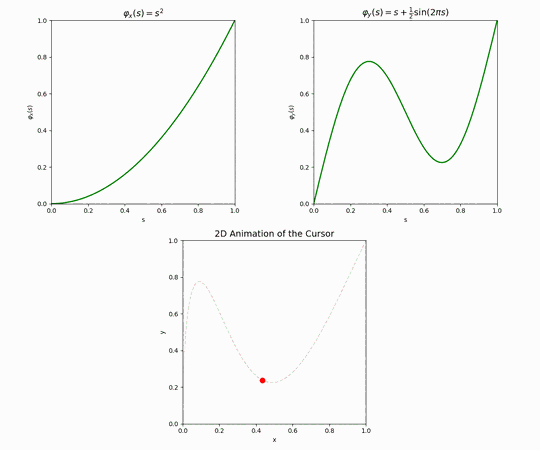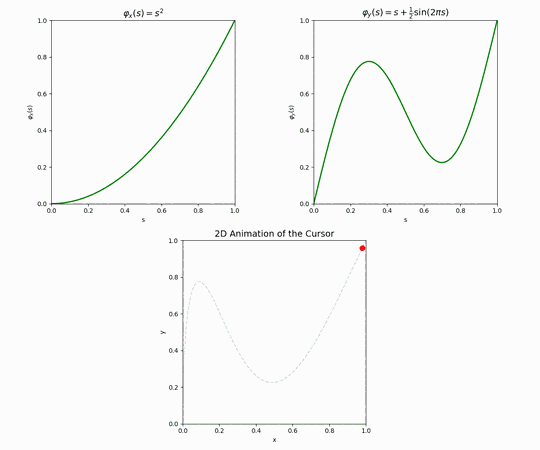
Once a source point and a destination point on the screen are chosen, as well as path prototypes for both the \(x\) and \(y\) coordinates and a desired time for the trip to take place, creating the actual cursor movement is a matter of algebra — for each point in time seeing what portion \(0 \leq r \leq 1\) of the trip has elapsed, what values the prototypes \(\varphi_x\) and \(\varphi_y\) take at that \(r\), and finally computing the corresponding linear combinations of \(v_{\text{cur}}\) and \(v_{\text{next}}\) at the \(x\) coordinate and \(y\) coordinate.

Let’s see an example. Suppose we are charting a path between two points on a 1920×1080 display. We have determined that the journey should take \(T= 5_{\text{sec}}\). Using the above method, we generate path prototypes, one per each coordinate.

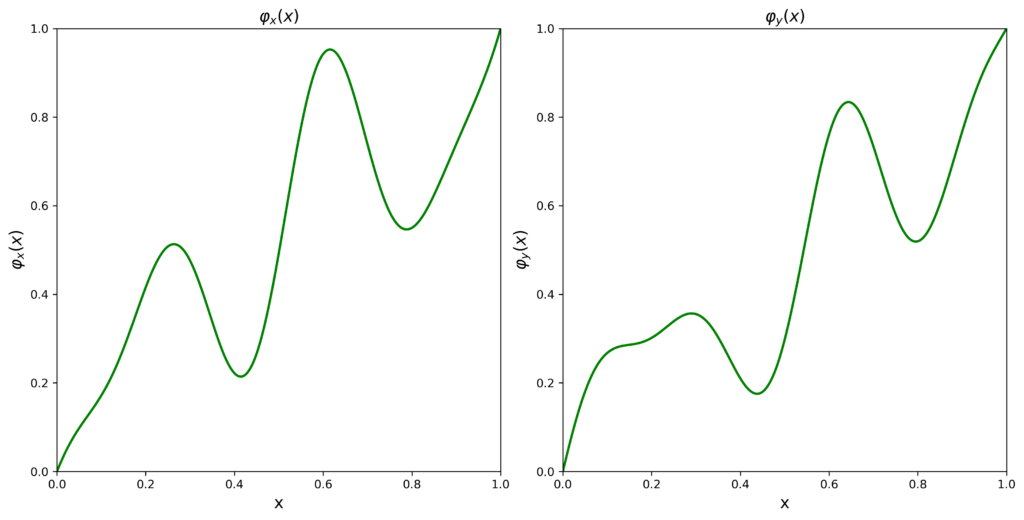
Applying these two prototypes to the movement between \(v_{\text{cur}}\) and \(v_{\text{next}}\), one then obtains the following cursor movement.

As explained earlier, the full simulated mouse movement is just a sequence of these paths, where the next destination is sampled from a Gaussian centered around the current position, and there is an exponentially distributed delay between one path and the next.

Feasibility of Counter-Counter-Evasions and so on

At this point, it is natural to ask how favorable the prospects are of an attacker trying to construct an evasion again, sidestepping a sandbox that employs this kind of simulated mouse movement. We think the answer is nuanced and is influenced mainly by the following considerations.

• The theoretical ceiling for the sophistication of evasions and counter-evasions in this space is very high. To intuitively understand this, consider that if a human tries to decide whether the mouse movement in the above animation is simulated or human-generated, there’s a decent chance they would answer correctly. But it won’t be so straightforward to properly motivate this answer or explain the considerations involved to a Python script.
• These sorts of games favor incremental improvement by their nature. There are many detections, mitigations, plays, and counter-plays where the thought of “What if my opponent plays their hand perfectly” is actively harmful. Usually, they won’t, and now, instead of taking advantage of this, you are helplessly staring at some esoteric and intractable general class of problem. It’s great to think about the holy grail of perfect solutions, but it’s often more practical to raise the bar and make attacks more of a hassle than before.
• As we get deeper into the game, diagnostic pressure on the attacker grows. This is, as we’ve already noted, a rare scenario where attackers are the ones who have to worry about false positives and false negatives. When we constructed our original evasion, we reached a very high degree of confidence. Specifically, we were able to programmatically quantify some concrete metric by which the simulation behaved in a way that no human ever would, with virtual certainty. When this degree of confidence is not within reach, the calculus changes. It’s not very clear what a malicious binary should do with, let’s say, 75% certainty that it’s running in a sandbox.
• We encourage you to do more than just copy-paste the code! Change the parameters, or even randomize reasonable values per run. Try another distribution for base_movement_time. Call generate_movement and interpolate the result with a bunch of other not-obviously-auto-generated stuff. Get creative. If there is no single algorithm to beat, attackers are at a further disadvantage.

Conclusion

The universe of sandbox evasions is very large and very strange. Even something as prosaic as minor quirks in a mouse movement can, in theory, spell the difference between a successful attack and an attack stopped in its tracks or between a targeted analysis taking an hour and taking half a week. Malware authors are doing their best to come up with new evasions all the time, and it’s hard to imagine a sweeping solution to all their many creative ideas. To win the day, defenders must take many Sisyphean small steps, closing half-open avenues and raising walls ever so slightly higher. The best we can hope for is that one day a malware author with a half-baked evasion idea on their mind reads this and says “never mind, I’m going to try something else”.

Appendix A: Full Code of Simulated Mouse Movement Module

import numpy as np
import random
import time
from math import floor,sqrt,sin,tau
from datetime import timedelta
from typing import Tuple, List, Callable
import platform

def get_display_resolution() -> Tuple[int,int]:
    if platform.system() == 'Windows':
        import ctypes
        user32 = ctypes.windll.user32
        user32.SetProcessDPIAware()
        return user32.GetSystemMetrics(0), user32.GetSystemMetrics(1)
    if platform.system() == 'Linux':
        from Xlib.display import Display
        screen = Display(':0').screen()
        return (screen.width_in_pixels, screen.height_in_pixels)
    print("Could not get screen resolution.")
    exit(1)

#parameters

#All time intervals are in ms
class TIME:
    MS_IN_S = 1000
    INTERVAL = 10

class MOV:
    GLOBAL_COEF = 15000
    MIN_TIME = 100
    EXP_DIST_MEAN = 1
    DEST_MOTILITY = 0.25

class WAIT:
    GLOBAL_COEF = 500
    EXP_DIST_MEAN = 1

class SCR:
    WIDTH, HEIGHT = get_display_resolution()

class PROTO:
    MAX_FREQ = 4
    NUM_WAVES = 6

type Coor = List[int]
type Prototype = Callable[[float],float]

#functions

def generate_movement(t: timedelta) -> List[Coor]:
    output_len = int(floor((t.total_seconds() * TIME.MS_IN_S) / TIME.INTERVAL))
    result : List[Coor] = []
    cur_pos : Coor = gauss_step_from(
        [SCR.WIDTH//2,SCR.HEIGHT//2],
        [SCR.WIDTH,SCR.HEIGHT]
    )
    while len(result) < output_len:
        #move
        next_pos = gauss_step_from(cur_pos,[SCR.WIDTH,SCR.HEIGHT])
        mov_time = pick_movement_time(cur_pos,next_pos)
        mov_steps = time_to_steps(mov_time)
        path = gen_path(cur_pos,next_pos,mov_steps)
        result += path
        
        #wait
        wait_time = timedelta(milliseconds=np.random.exponential(WAIT.EXP_DIST_MEAN)*WAIT.GLOBAL_COEF)
        wait_steps = time_to_steps(wait_time)
        result += [result[-1]]*wait_steps

        cur_pos = next_pos
    
    result = result[:output_len]
    return result

def time_to_steps(t: timedelta) -> int:
    return int(floor(t.total_seconds()*TIME.MS_IN_S / TIME.INTERVAL))

def pick_movement_time(cur_pos: Coor, next_pos: Coor) -> timedelta:
    mlc = mov_len_coef(cur_pos,next_pos)
    base_movement_time = np.random.exponential(MOV.EXP_DIST_MEAN)
    return timedelta(milliseconds=max(
        MOV.MIN_TIME,
        base_movement_time*mlc*MOV.GLOBAL_COEF
    ))

def gauss_step_from(src: Coor, bound: Coor) -> Coor:
    assert len(src)==len(bound)
    dim = len(src)
    assert(0 < MOV.DEST_MOTILITY <= 0.5)
    assert(all([0<=src[i]<=bound[i] for i in range(dim)]))
    
    def gauss_step_1d(src,bound):
        result = None
        while not result or not 0 < result < bound:
            result = round(np.random.normal(src, bound*MOV.DEST_MOTILITY)) 
        return result

    return [gauss_step_1d(src[i],bound[i]) for i in range(len(src))]

def mov_len_coef(src: Coor,dst: Coor) -> float:
    abs_dist =  sqrt((dst[0]-src[0])**2+(dst[1]-src[1])**2)
    screen_diag = sqrt(SCR.WIDTH**2+SCR.HEIGHT**2)
    return abs_dist / screen_diag

    
def gen_path_proto_1d() -> Prototype:
    wave = lambda n,shift: lambda x: sin(n*tau*x+shift)
    freqs = [random.choice(range(1,PROTO.MAX_FREQ+1)) for _ in range(PROTO.NUM_WAVES)]
    profile = {f:np.random.uniform()*tau for f in freqs}
    h = lambda x: sum([wave(f,s)(x) for (f,s) in profile.items()])/len(profile)
    psi = lambda x: 4*(x-x**2)
    f = lambda x: x*(1-psi(x))+((h(x)+1)/2)*psi(x)
    return f

def actualize_path_1d(proto: Prototype, start: int, end: int, steps: int) -> List[int]:
    r = lambda i: proto(i/steps)
    samples = steps+1 # @---@---@---@ ||| ---*3 whereas @*(3+1)
    return [round(start*(1-r(i)) + end*r(i)) for i in range(samples)]

def gen_path(src: Coor, dst: Coor, steps: int) -> List[Coor]:
    assert(len(src)==len(dst))
    dim = len(src)
    protos = [gen_path_proto_1d() for _ in range(dim)]
    path = [actualize_path_1d(protos[i],src[i],dst[i],steps) for i in range(dim)]
    return list(np.transpose(path))

def demo(coors: List[Coor]):
    from pynput.mouse import Controller
    mouse = Controller()
    for coor in coors:
        mouse.position = coor
        time.sleep(TIME.INTERVAL/TIME.MS_IN_S)

if __name__ == "__main__":
    coors = generate_movement(timedelta(seconds=30))
    demo(coors)